Parallelismo di piani: un segno, una condizione
Chiunque abbia mai studiato o stia studiando a scuola ha dovuto affrontare varie difficoltà nello studio delle discipline incluse nel programma sviluppato dal Ministero della Pubblica Istruzione.
Quali difficoltà devono affrontare
L'apprendimento delle lingue è accompagnato dalla memorizzazione delle regole grammaticali esistenti e delle principali eccezioni a esse. L'educazione fisica richiede una grande quantità di calcoli, forma fisica e grande pazienza da parte degli studenti.
Tuttavia, è impossibile confrontare con qualsiasi cosa le difficoltà che sorgono quando si studiano discipline esatte. Algebra contenente modi complessi per risolvere problemi elementari. Fisica con un ricco insieme di formule di leggi fisiche. La geometria e le sue sezioni, che sono basate su teoremi e assiomi complessi.
Un esempio sono gli assiomi che spiegano la teoria del parallelismo dei piani, che devono essere necessariamente ricordati, poiché sono alla base dell'intero corso del programma scolastico in stereometria. Proviamo a capire quanto sia più facile e veloce ciò che si può fare.
Piani paralleli con esempi
L'assioma, che indica il parallelismo dei piani, recita come segue: " Qualsiasi due piani sono considerati paralleli solo se non contengono punti comuni ", cioè non si intersecano l'uno con l'altro. Per immaginare questa immagine in modo più dettagliato, come esempio elementare, possiamo dare il rapporto tra il soffitto e il pavimento o le pareti opposte di un edificio. Diventa immediatamente chiaro cosa si intende, e conferma anche il fatto che nel solito caso questi piani non si intersecano mai.
Un altro esempio è una vetrata, in cui le reti di vetro fungono da piani. Inoltre, in nessun caso formeranno punti di intersezione. Inoltre, è possibile aggiungere scaffali, il cubo di Rubik, dove i piani sono i lati opposti e altri elementi della vita quotidiana.
Gli aerei in questione sono designati da un segno speciale sotto forma di due linee rette "||", che illustrano chiaramente il parallelismo dei piani. Quindi, applicando esempi reali, si può formare una percezione più chiara dell'argomento e, di conseguenza, si può procedere oltre alla considerazione di concetti più complessi.
Dove e come viene applicata la teoria dei piani paralleli?
Quando si studia un corso scolastico in geometria, gli studenti devono affrontare problemi a molti lati, dove è spesso necessario determinare il parallelismo di linee, linee e piani tra loro o la dipendenza dei piani l'uno dall'altro. Analizzando la condizione esistente, ogni attività può essere correlata alle quattro classi principali di stereometria.
La prima classe include compiti in cui è necessario determinare il parallelismo di una linea e di un piano tra di loro. La sua soluzione si riduce a dimostrare il teorema con lo stesso nome. Per fare ciò, è necessario determinare se esiste una retta parallela che giace in questo piano per una linea retta che non appartiene al piano in questione.
La seconda classe di compiti include quelli in cui è coinvolta la funzionalità del parallelismo dei piani. Viene utilizzato per semplificare il processo di prova, riducendo in modo significativo il tempo necessario per trovare una soluzione.
La prossima classe copre la gamma di problemi di conformità con le proprietà di base dirette del parallelismo dei piani. La soluzione dei problemi della quarta classe consiste nel determinare se la condizione del parallelismo dei piani è soddisfatta. Sapendo esattamente come si verifica la prova di un particolare problema, diventa più facile per gli studenti navigare quando si utilizza il proprio arsenale di assiomi geometrici.
Pertanto, i compiti, la cui condizione richiede la definizione e la dimostrazione del parallelismo delle linee rette, una retta e un piano o due piani tra di loro, sono ridotti alla selezione corretta del teorema e della soluzione in base al set di regole esistente.
Informazioni sul parallelismo di una linea e un piano
Il parallelismo di una retta e di un piano è un argomento speciale nella stereometria, poiché è questo il concetto di base su cui si basano tutte le proprietà successive del parallelismo delle figure geometriche.
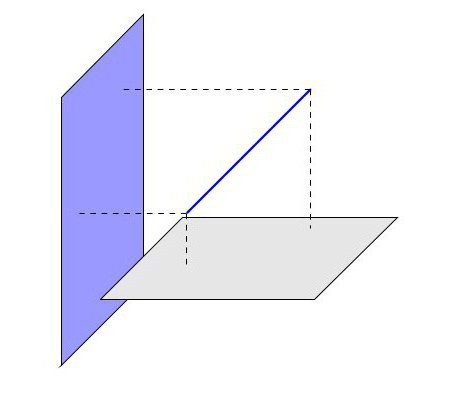
Secondo gli assiomi esistenti, nel caso in cui due punti di una retta appartengono a un certo piano, possiamo concludere che anche questa linea retta si trova in esso. In questa situazione, diventa chiaro che ci sono tre opzioni per la posizione di una linea retta rispetto a un piano nello spazio:
- La linea appartiene all'aereo.
- Per una linea retta e un piano c'è un punto di intersezione comune.
- Per una linea retta e un piano, i punti di intersezione sono assenti.
In particolare, siamo interessati alla seconda opzione, quando non ci sono punti di intersezione. Solo allora possiamo dire che la retta e il piano sono tra loro paralleli. Quindi, viene confermata la condizione del teorema principale sul segno parallelo di una retta e di un piano, che afferma che: "Se una retta che non appartiene al piano in questione è parallela a qualsiasi retta su questo piano, allora anche la retta è parallela al piano dato".
La necessità di utilizzare la funzionalità del parallelismo
Il segno del parallelismo degli aerei, di regola, viene utilizzato per cercare una soluzione semplificata dei problemi relativi ai piani. L'essenza di questa funzione è la seguente: " Se ci sono due linee rette che si intersecano in un piano, parallele a due linee rette appartenenti ad un altro piano, allora tali piani possono essere chiamati paralleli ".
Teoremi aggiuntivi
Oltre ad usare il segno che prova il parallelismo degli aerei, in pratica puoi incontrare l'uso di altri due teoremi aggiuntivi. Il primo è presentato nella seguente forma: " Se uno dei due piani paralleli è parallelo al terzo, il secondo piano è parallelo al terzo o coincide completamente con esso ".
Basato sull'uso di teoremi riducibili, si può sempre dimostrare il parallelismo degli aerei rispetto allo spazio preso in considerazione. Il secondo teorema mostra la dipendenza dei piani sulla retta perpendicolare e assomiglia a: " Se due piani non coincidenti sono perpendicolari rispetto ad alcune rette, allora sono considerati paralleli tra loro ".
La nozione di condizioni necessarie e sufficienti
Nel risolvere i problemi di provare il parallelismo dei piani più volte, è stata derivata la condizione necessaria e sufficiente per il parallelismo dei piani. È noto che qualsiasi piano è dato da un'equazione parametrica della forma: A 1 x + B 1 y + C 1 z + D 1 = 0. La nostra condizione si basa sull'uso di un sistema di equazioni che definiscono la disposizione dei piani nello spazio ed è rappresentata dal seguente testo: " Per provare il parallelismo di due piani, è necessario e sufficiente che il sistema di equazioni che descrivono questi piani sia incompatibile, cioè non abbia soluzione ."
Proprietà di base
Tuttavia, quando si risolvono problemi geometrici, l'uso della funzionalità del parallelismo non è sempre sufficiente. A volte una situazione sorge quando è necessario dimostrare il parallelismo di due o più linee in piani diversi o l'uguaglianza dei segmenti racchiusi su queste linee. Per fare ciò, applica le proprietà dei piani paralleli. In geometria, ce ne sono solo due.
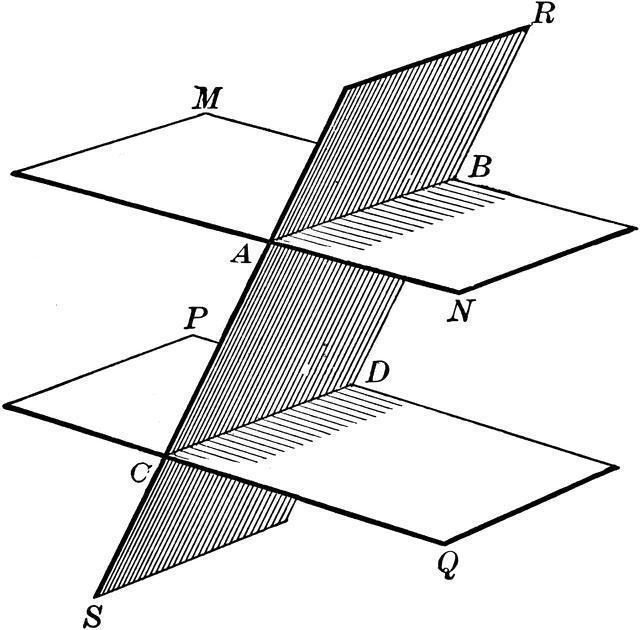
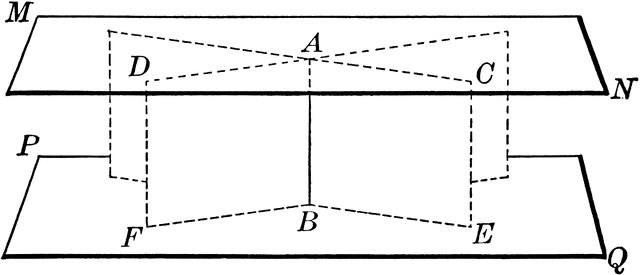
La prima proprietà ci consente di giudicare il parallelismo delle linee in alcuni piani e viene presentato nella seguente forma: " Se due piani paralleli intersecano il terzo, allora anche le linee formate dalle linee di intersezione saranno parallele l'una all'altra ".
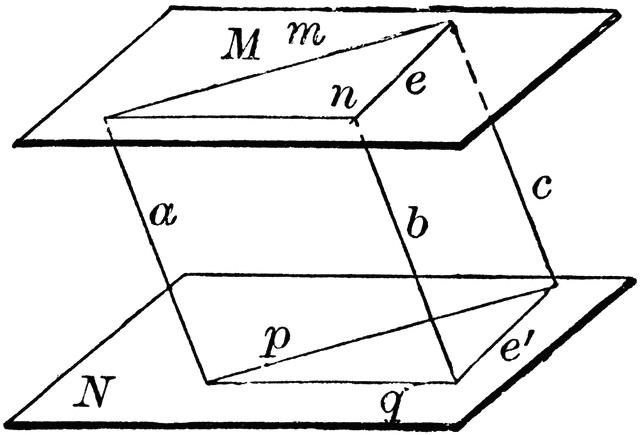
Il significato della seconda proprietà è di dimostrare l'uguaglianza dei segmenti situati su linee rette parallele. La sua interpretazione è presentata di seguito. " Se consideriamo due piani paralleli e racchiudiamo una regione tra loro, allora si può sostenere che la lunghezza dei segmenti formati da questa regione sarà la stessa ."