Periodo di oscillazione: esperimenti, formule, compiti

Qual è il periodo di oscillazione? Qual è questo valore, che senso fisico ha e come calcolarlo? In questo articolo tratteremo questi problemi, considereremo le varie formule con cui è possibile calcolare il periodo di oscillazione e scopriremo quale relazione esiste tra tali quantità fisiche come il periodo e la frequenza di oscillazione del corpo / sistema.

Definizione e significato fisico

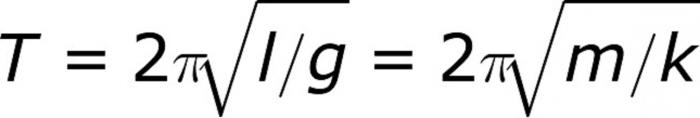
Il periodo di oscillazione è chiamato un tale periodo in cui il corpo o il sistema esegue una oscillazione (necessariamente completa). In parallelo, è possibile notare il parametro a cui l'oscillazione può essere considerata completa. Il ruolo di tale condizione è il ritorno del corpo al suo stato originale (alla coordinata originale). Un'ottima analogia con il periodo della funzione. A proposito, è un errore pensare che avvenga esclusivamente nella matematica ordinaria e superiore. Come sai, queste due scienze sono inestricabilmente legate. E il periodo delle funzioni può essere incontrato non solo quando si risolvono le equazioni trigonometriche, ma anche in varie sezioni di fisica, vale a dire, stiamo parlando di meccanica, ottica e altri. Quando si trasferisce il periodo delle oscillazioni dalla matematica alla fisica, è necessario comprendere solo una quantità fisica (e non una funzione), che dipende direttamente dal tempo che passa.

Quali sono le fluttuazioni?

Le oscillazioni sono divise in armoniche e anarmoniche, oltre che periodiche e non periodiche. Sarebbe logico presumere che nel caso delle oscillazioni armoniche, vengano eseguite secondo alcune funzioni armoniche. Può essere sia un seno che un coseno. In questo caso, potrebbero esserci coefficienti di compressione-allungamento e aumento-diminuzione. Inoltre, le oscillazioni sono smorzate. Cioè, quando una certa forza agisce sul sistema, che gradualmente "rallenta" le oscillazioni stesse. Allo stesso tempo, il periodo diventa più piccolo, mentre la frequenza di oscillazione è in costante aumento. Molto bene dimostra un assioma così semplice dell'esperienza fisica con l'uso di un pendolo. Può essere di tipo primaverile, oltre che matematico. Non importa. A proposito, il periodo di oscillazione in tali sistemi sarà determinato da diverse formule. Ma ne parleremo più avanti. Ora diamo esempi.

Esperienza con i pendoli

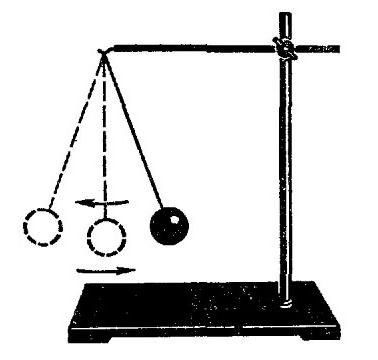
Ogni pendolo può essere preso per primo, non ci sarà differenza. Le leggi della fisica e le leggi della fisica, che sono rispettate in ogni caso. Ma per qualche ragione più come il pendolo matematico. Se qualcuno non sa cosa sia: si tratta di una palla su un filo inestensibile attaccato a una barra orizzontale attaccata alle gambe (o elementi che svolgono il loro ruolo - per mantenere il sistema in equilibrio). La palla è meglio prendere dal metallo, in modo che l'esperienza fosse più chiara.

Quindi, se porti un bilanciamento di tale sistema, applica una certa forza alla palla (in altre parole, spingila), quindi la palla inizierà a oscillare sul filo, seguendo una certa traiettoria. Col passare del tempo, noterai che la traiettoria lungo la quale passa la palla diminuisce. Allo stesso tempo, la palla inizia a muoversi avanti e indietro sempre più velocemente. Questo suggerisce questo frequenza di oscillazione aumenta. Ma il tempo per cui la palla ritorna alla sua posizione iniziale diminuisce. Ma il tempo di un'oscillazione completa, come abbiamo scoperto prima, è chiamato periodo. Se un valore diminuisce e l'altro aumenta, allora parliamo di proporzionalità inversa. Quindi siamo arrivati ​​al primo punto, sulla base del quale sono state costruite le formule per determinare il periodo di oscillazione. Se prendiamo il pendolo a molla, allora la legge sarà osservata lì in una forma leggermente diversa. Perché sia ​​rappresentato in modo più chiaro, porteremo il sistema in movimento su un piano verticale. Per renderlo più chiaro, inizialmente valeva la pena di dire che cos'è il pendolo a molla. Dal nome è chiaro che una primavera deve essere presente nel suo design. E questo è vero. Di nuovo, abbiamo un piano orizzontale sui supporti, a cui è sospesa una molla di una certa lunghezza e rigidità. A lei, a sua volta, viene sospeso il peso. Può essere un cilindro, un cubo o un'altra figura. Potrebbe anche essere un elemento di terze parti. In ogni caso, quando si rimuove il sistema dalla posizione di equilibrio, inizierà a fare oscillazioni smorzate. L'aumento più evidente della frequenza è nel piano verticale, senza alcuna deviazione. Con questo con gli esperimenti puoi finire.

Quindi, nel loro corso, abbiamo scoperto che il periodo e la frequenza delle oscillazioni sono due quantità fisiche che hanno una relazione inversa.

Designazione di quantità e dimensioni

Di solito il periodo di oscillazione è denotato dalla lettera latina T. Molto meno spesso può essere indicato diversamente. La frequenza è indicata dalla lettera μ ("Mu"). Come abbiamo detto all'inizio, un periodo non è altro che un tempo in cui si verifica un'oscillazione completa nel sistema. Quindi la dimensione del periodo sarà seconda. E poiché il periodo e la frequenza sono inversamente proporzionali, allora la dimensione della frequenza sarà divisa per il secondo. Nelle registrazioni delle attività, tutto sarà simile a questo: T (s), μ (1 / s).

Formula per il pendolo matematico. Problema numero 1

Come nel caso degli esperimenti, ho deciso prima di tutto di occuparmi del pendolo matematico. Non entreremo nella derivazione della formula in dettaglio, poiché tale compito non era inizialmente impostato. E la conclusione di per sé è ingombrante. Ma diamo un'occhiata alle formule stesse, scopriamo quali sono i valori in esse contenuti. Quindi, la formula per il periodo di oscillazione per un pendolo matematico è la seguente:

Dove l - la lunghezza del filo, n = 3.14 e g - accelerazione caduta libera (9,8 m / s ^ 2). La formula non dovrebbe causare alcuna difficoltà. Pertanto, senza ulteriori domande, procediamo immediatamente a risolvere il problema di determinare il periodo di oscillazione del pendolo matematico. Una palla di metallo del peso di 10 grammi è sospesa su un filo inestensibile lungo 20 centimetri. Calcola il periodo di oscillazione del sistema, considerandolo come un pendolo matematico. La soluzione è molto semplice. Come in tutti i problemi di fisica, è necessario semplificarlo il più possibile a causa del rifiuto di parole non necessarie. Sono inclusi nel contesto al fine di confondere il decisore, ma in realtà non hanno assolutamente alcun peso. Nella maggior parte dei casi, ovviamente. Qui puoi escludere il momento con "thread inestensibile". Questa frase non dovrebbe entrare in uno stato di torpore. E poiché abbiamo un pendolo matematico, non dovremmo essere interessati alla massa del carico. Cioè, le parole di circa 10 grammi hanno anche lo scopo di confondere lo studente. Ma sappiamo che non c'è massa nella formula, quindi con la coscienza pulita possiamo procedere alla decisione. Quindi, prendiamo la formula e semplicemente sostituiamo i valori in essa, poiché è necessario determinare il periodo del sistema. Poiché non sono state specificate condizioni aggiuntive, arrotonderemo i valori al 3 ° decimale, come è consuetudine. Moltiplicando e dividendo i valori, otteniamo che il periodo di oscillazione sia 0.886 secondi. Problema risolto

Formula per il pendolo a molla. Problema numero 2

Le formule dei pendoli hanno una parte comune, vale a dire 2p. Questo valore è presente in due formule contemporaneamente, ma differiscono per un'espressione radicale. Se nel problema relativo al periodo del pendolo a molla viene indicato il peso del carico, è impossibile evitare calcoli con la sua applicazione, come nel caso del pendolo matematico. Ma non dovresti aver paura. Ecco la formula del periodo per il pendolo a molla:

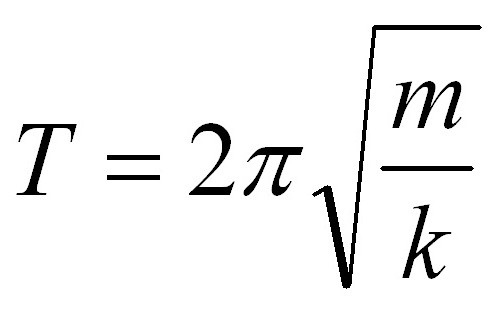
In esso, m è la massa del carico sospeso dalla molla, k è la costante di molla della molla. Nell'attività, è possibile fornire il valore del coefficiente. Ma se nella formula del pendolo matematico non ti stai chiarendo particolarmente - dopo tutto, 2 di 4 valori sono costanti - allora viene aggiunto il parametro 3, che può essere modificato. E all'uscita abbiamo 3 variabili: il periodo (frequenza) delle oscillazioni, la costante di molla della molla, la massa del carico sospeso. L'attività può essere orientata alla ricerca di uno qualsiasi di questi parametri. Sarebbe troppo facile guardare di nuovo per un periodo, quindi cambieremo le condizioni un po '. Trova il coefficiente di rigidità della molla se il tempo di oscillazione totale è di 4 secondi e il peso del carico del pendolo a molla è di 200 grammi.

Per risolvere qualsiasi problema fisico, sarebbe bene prima disegnare un'immagine e scrivere formule. Sono metà della battaglia qui. Scrivendo una formula, è necessario esprimere il coefficiente di rigidità. Lo abbiamo sotto la radice, quindi radicheremo entrambi i lati dell'equazione. Per eliminare la frazione, moltiplica le parti per k. Ora lasciamo solo il coefficiente sul lato sinistro dell'equazione, cioè dividiamo le parti per T ^ 2. In linea di principio, il compito potrebbe essere un po 'più difficile, non impostare il periodo nei numeri, ma la frequenza. In ogni caso, durante il calcolo e l'arrotondamento (abbiamo concordato di arrotondare alla terza cifra decimale), risulta che k = 0, 157 N / m.

Il periodo di oscillazioni libere. La formula del periodo di oscillazioni libere

Sotto la formula del periodo vibrazioni libere capire le formule che abbiamo risolto nei due problemi citati in precedenza. Anche l'equazione delle vibrazioni libere è compilata, ma stiamo già parlando di spostamenti e coordinate, e questa domanda si riferisce ad un altro articolo.

Suggerimenti per risolvere i problemi legati al periodo

1) Prima di intraprendere un'attività, annotare la formula ad essa associata.

2) I compiti più semplici non richiedono immagini, ma in casi eccezionali dovranno essere eseguiti.

3) Cerca di sbarazzarti delle radici e dei denominatori, se possibile. L'equazione scritta in linea, senza denominatore, è molto più facile e più facile da risolvere.