Segni, elementi costitutivi e proprietà di un triangolo isoscele

I primi storici della nostra civiltà - gli antichi greci - menzionano l'Egitto come il luogo di nascita della geometria. È difficile non essere d'accordo con loro, sapendo con quale tremenda precisione sono state erette le gigantesche tombe dei faraoni. La disposizione reciproca dei piani piramidali, le loro proporzioni, l'orientamento lungo i punti cardinali - sarebbe inconcepibile per raggiungere tale perfezione senza conoscere le basi della geometria.

La parola "geometria" può essere tradotta come "la dimensione della terra". E la parola "terra" non appare come un pianeta - parte del sistema solare, ma come un piano. La marcatura delle aree per l'agricoltura, molto probabilmente, è la base iniziale della scienza delle forme geometriche, dei loro tipi e proprietà.

Un triangolo è la più semplice figura spaziale della planimetria, contenente solo tre punti: i vertici (non ci può essere niente di meno). La base delle basi potrebbe essere il motivo per cui in essa appare qualcosa di misterioso e antico. L'occhio onniveggente all'interno del triangolo è uno dei primi segni occulti conosciuti, e la geografia della sua distribuzione e il suo calendario sono semplicemente stupefacenti. Dall'antico Egitto, Sumero, Azteco e altre civiltà alle più moderne comunità di amanti occulti, sparsi in tutto il mondo.

Quali sono i triangoli

Un triangolo versatile regolare è una figura geometrica chiusa costituita da tre segmenti di diverse lunghezze e tre angoli, nessuno dei quali è giusto. Oltre a ciò, ci sono diversi tipi speciali.

Il triangolo acuto ha tutti gli angoli inferiori a 90 gradi. In altre parole, tutti gli angoli di tale triangolo sono nitidi.

Triangolo rettangolo su cui gli scolari hanno pianto in ogni momento a causa dell'abbondanza di teoremi, ha un angolo con una magnitudine di 90 gradi o, come viene anche chiamato, una linea retta.

Il triangolo ottuso si distingue per il fatto che uno dei suoi angoli è ottuso, cioè la sua magnitudine è maggiore di 90 gradi.

Il triangolo equilatero ha tre lati della stessa lunghezza. Una tale figura ha anche tutti gli angoli.

Infine, in un triangolo isoscele di tre lati, i due sono uguali.

Caratteristiche distintive

Le proprietà di un triangolo isoscele determinano anche la differenza principale, principale: l'uguaglianza dei due lati. Questi lati uguali tra loro sono chiamati cosce (o, più spesso, lati laterali), ma la terza parte è chiamata "fondazione".

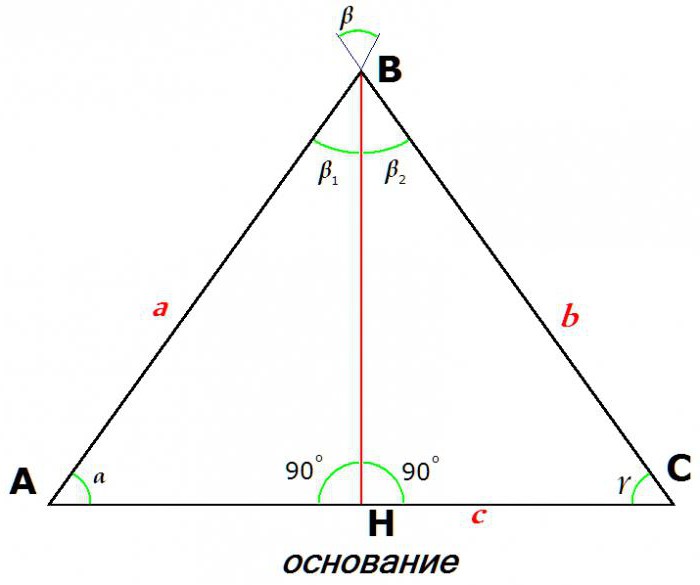
In questa figura, a = b.

Il secondo segno di un triangolo isoscele segue il teorema del seno. Poiché i lati aeb sono uguali, i seni dei loro angoli opposti sono uguali:

a / sin γ = b / sin α, donde abbiamo: sin γ = sin α.

L'uguaglianza dei seni implica l'uguaglianza degli angoli: γ = α.

Quindi, il secondo segno di un triangolo isoscele è l'uguaglianza di due angoli adiacenti alla base.

Il terzo segno. Il triangolo distingue elementi come altezza, bisettrice e mediana.

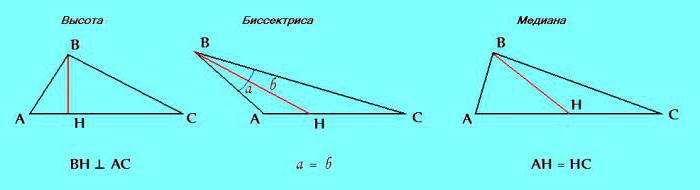
Se nel processo di risoluzione del problema si scopre che nel triangolo considerato due di questi elementi sono gli stessi: altezza con bisettrice; bisettrice con mediana; mediano con altezza - è sicuramente possibile concludere che il triangolo è isoscele.

Proprietà geometriche della figura

1. Proprietà di un triangolo isoscele. Una delle qualità distintive della figura è l'uguaglianza degli angoli adiacenti alla base:

α = γ;

<TU = <BCA.

2. Un'altra proprietà discussa sopra: la mediana, la bisettrice e l'altezza in un triangolo isoscele coincidono se sono costruite dal suo vertice alla base.

3. Uguaglianza delle bisettrici tratte dai vertici alla base:

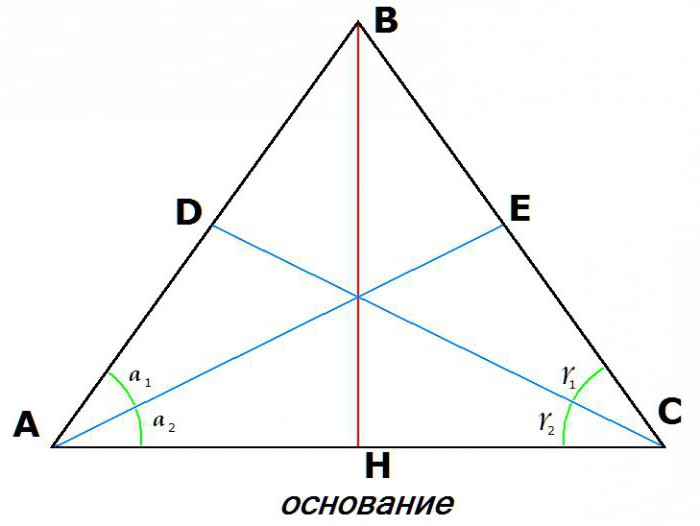
Se AE è la bisettrice dell'angolo YOU, e CD è la bisettrice dell'angolo BCA, quindi: AE = DC.

4. Le proprietà di un triangolo isoscele forniscono anche l'uguaglianza delle altezze che vengono tratte dai vertici alla base.

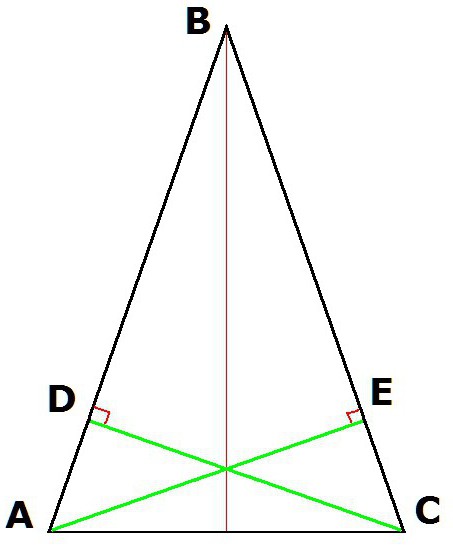
Se costruiamo le altezze del triangolo ABC (dove AB = BC) dai vertici A e C, allora i segmenti risultanti CD ed AE saranno uguali.

5. Anche le mediane disegnate dagli angoli alla base saranno uguali.

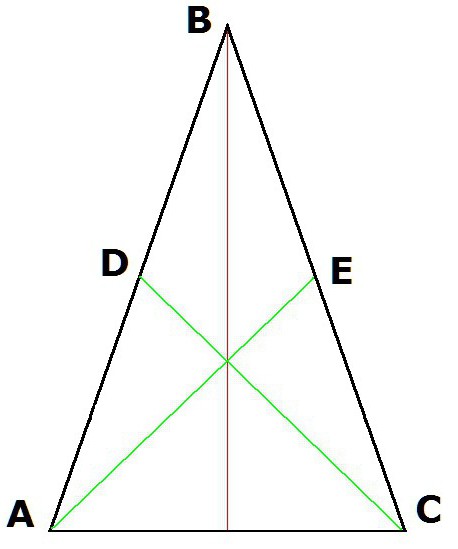
Quindi, se AE e DC sono mediani, cioè AD = DB e BE = EC, quindi AE = DC.

Altezza triangolo isoscele

L'uguaglianza dei lati e degli angoli a loro aggiunge alcune peculiarità al calcolo delle lunghezze degli elementi della figura in esame.

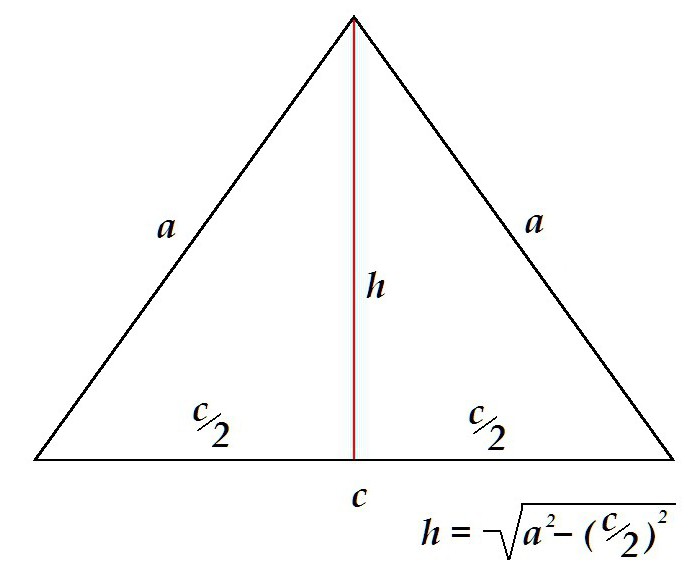
L'altezza in un triangolo isoscele divide la figura in 2 triangoli simmetrici ad angolo retto con ipotenus in cui i lati proiettano. L'altezza in questo caso è determinata dal teorema di Pitagora come una gamba.

Un triangolo può avere tutti e tre i lati uguali, quindi sarà chiamato equilatero. L'altezza in un triangolo equilatero è determinata nello stesso modo, solo per i calcoli è sufficiente conoscere un solo valore - la lunghezza del lato di questo triangolo.

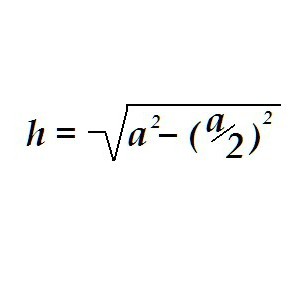
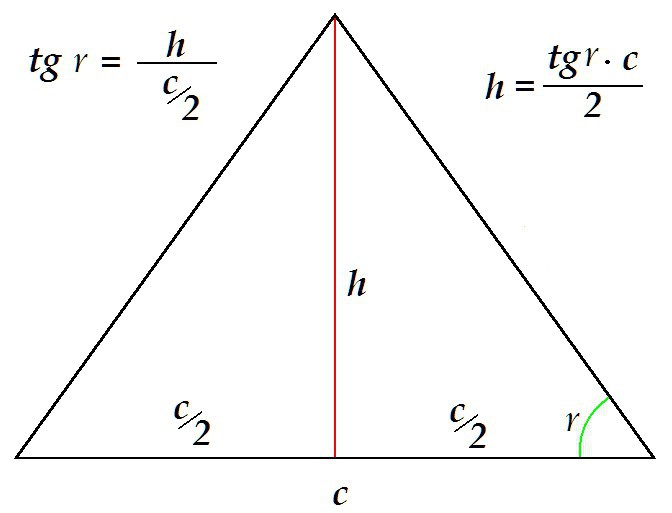
È possibile determinare l'altezza in un altro modo, ad esempio conoscendo la base e l'angolo adiacente ad essa.

Mediana di un triangolo isoscele

Il tipo considerato di un triangolo, a causa delle sue caratteristiche geometriche, è risolto semplicemente dall'insieme minimo di dati sorgente. Poiché la mediana in un triangolo isoscele è uguale sia alla sua altezza che alla sua bisettrice, l'algoritmo per determinarlo non è diverso dall'ordine in cui questi elementi sono calcolati.

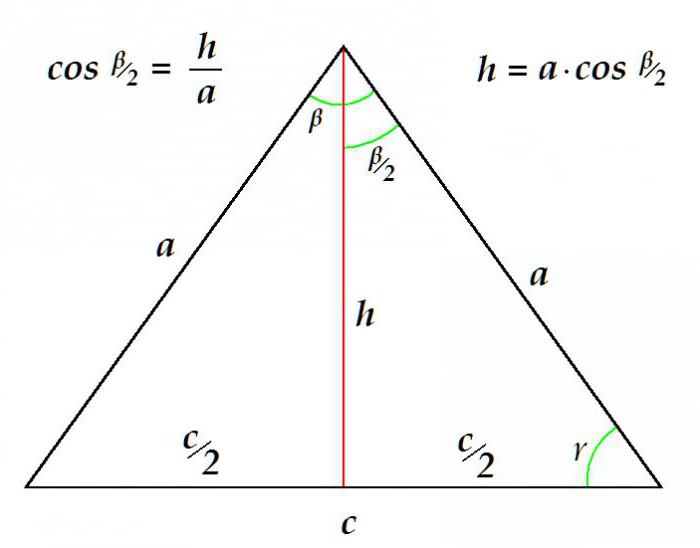
Ad esempio, è possibile determinare la lunghezza della mediana per il lato noto e l'angolo al vertice.

Come determinare il perimetro

Poiché nella figura planimetrica considerata i due lati sono sempre uguali, quindi per determinare il perimetro è sufficiente conoscere la lunghezza della base e la lunghezza di uno dei lati.

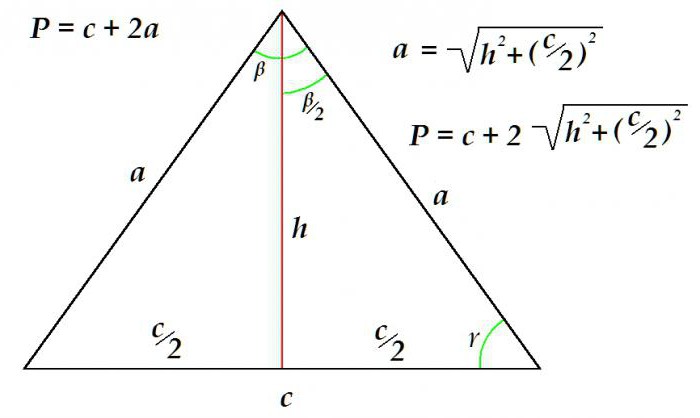
Considera un esempio quando definirlo perimetro di un triangolo dalla nota base e altezza.

Il perimetro è uguale alla somma della base e il doppio della lunghezza del lato. Il lato, a sua volta, è determinato usando il teorema di Pitagora come l'ipotenusa di un triangolo rettangolo. La sua lunghezza è uguale a radice quadrata della somma del quadrato di altezza e del quadrato di metà della base.

Area di un triangolo isoscele

Ci sono, di regola, difficoltà e il calcolo dell'area di un triangolo isoscele. La regola universale per determinare l'area di un triangolo come metà del prodotto della base alla sua altezza si applica, ovviamente, anche nel nostro caso. Tuttavia, le proprietà di un triangolo isoscele rendono l'attività più facile.

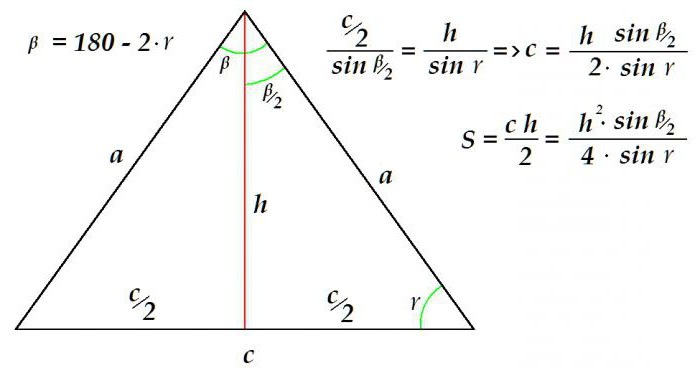
Supponiamo che l'altezza e l'angolo adiacenti alla base siano noti. È necessario determinare l'area della figura. Questo può essere fatto in questo modo.

Poiché la somma degli angoli di qualsiasi triangolo è 180 °, è facile determinare l'angolo. Inoltre, usando la proporzione elaborata secondo il teorema del seno, viene determinata la lunghezza della base del triangolo. Tutto, la base e l'altezza - dati sufficienti per la determinazione dell'area - sono disponibili.

Altre proprietà di un triangolo isoscele

La posizione del centro di un cerchio descritta attorno a un triangolo isoscele dipende dall'angolo del vertice. Quindi, se un triangolo isoscele è acuto, il centro del cerchio si trova all'interno della figura.

Il centro del cerchio, che è descritto attorno a un triangolo isoscele a punta ottusa, si trova al di fuori di esso. E infine, se l'angolo al vertice è di 90 °, il centro si trova esattamente al centro della base e il diametro del cerchio passa attraverso la base stessa.

Per determinare il raggio di un cerchio descritto attorno a un triangolo isoscele, è sufficiente dividere la lunghezza del lato per il doppio coseno di metà dell'angolo sul vertice.