Area trapezoidale: formule e metodi di calcolo

Per sentirsi fiduciosi e risolvere con successo i problemi nelle lezioni di geometria, non è sufficiente imparare le formule. Devono prima capire. Avere paura, e ancor di più odiare le formule, è improduttivo. In questo articolo, la lingua disponibile analizzerà vari modi per trovare l'area di un trapezio. Per una migliore padronanza delle regole e dei teoremi pertinenti, presteremo attenzione alle sue proprietà. Ciò aiuterà a capire come funzionano le regole e in quali casi queste o quelle formule dovrebbero essere applicate.

Determina il trapezio

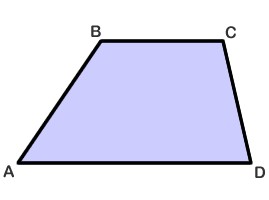Qual è questa figura in generale? Un trapezio è un poligono da quattro angoli con due lati paralleli. Gli altri due lati del trapezio possono essere inclinati a diverse angolazioni. I suoi lati paralleli sono chiamati basi, e per i lati non paralleli, viene usato il nome "lati" o "fianchi". Tali figure sono abbastanza comuni nella vita di tutti i giorni. I contorni del trapezio possono essere visti nelle sagome di vestiti, oggetti interni, mobili, piatti e molti altri. Un trapezio può essere di diversi tipi: versatile, equilatero e rettangolare. Maggiori dettagli sui loro tipi e proprietà saranno discussi più avanti nell'articolo.

Proprietà trapezoidali

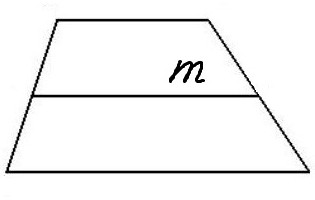Cerchiamo di discutere brevemente le proprietà di questa figura. La somma degli angoli adiacenti ad entrambi i lati è sempre di 180 °. Va notato che tutti gli angoli del trapezio si sommano a 360 °. Il trapezio ha il concetto della linea di mezzo. Se colleghi i punti medi dei lati con un segmento, questa sarà la linea di mezzo. È designato m. La linea mediana ha delle proprietà importanti: è sempre parallela alle basi (ricordiamo che le basi sono anche parallele l'una all'altra) e pari alla loro metà-somma:

m = (a + b) / 2.

Questa definizione deve essere appreso e compreso, perché è la chiave per risolvere una moltitudine di problemi!

In un trapezio, puoi sempre abbassare l'altezza alla base. L'altezza è perpendicolare, spesso indicata dal simbolo h, che viene tracciata da qualsiasi punto di una base a un'altra base o alla sua continuazione. La linea mediana e l'altezza aiuteranno a trovare l'area del trapezio. Tali compiti sono i più comuni nel corso di geometria della scuola e appaiono regolarmente tra i documenti di prova e di esame.

Le formule più semplici di area trapezoidale

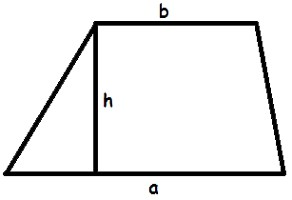Esaminiamo le due formule più popolari e semplici con cui l'aiuto trova l'area di un trapezio. È sufficiente moltiplicare l'altezza di una mezza somma di basi per trovare facilmente il desiderato:

S = h * (a + b) / 2.

In questa formula, a, b denota la base del trapezio, h - altezza. Per comodità di percezione, in questo articolo i segni di moltiplicazione sono contrassegnati con il simbolo (*) nelle formule, sebbene nei libri di riferimento ufficiali il segno di moltiplicazione di solito sia omesso.

Considera un esempio.

Dato: un trapezio con due basi pari a 10 e 14 cm, l'altezza è di 7 cm. Qual è l'area del trapezio?

Cerchiamo di analizzare la soluzione a questo problema. Secondo questa formula, devi prima trovare una mezza somma di basi: (10 + 14) / 2 = 12. Quindi, la mezza somma equivale a 12 cm. Ora moltiplichiamo la metà somma per l'altezza: 12 * 7 = 84. Il necessario è trovato. Risposta: l'area del trapezio è di 84 metri quadrati. cm.

La seconda formula ben nota dice: l'area di un trapezio è uguale al prodotto della linea centrale e all'altezza del trapezio. Questo, infatti, deriva dal concetto precedente della linea di mezzo: S = m * h.

Utilizzo di diagonali per i calcoli

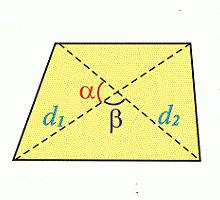
Un altro modo per trovare l'area trapezoidale non è in realtà così complicato. È associato alle sue diagonali. Secondo questa formula, per trovare l'area, è necessario moltiplicare il mezzo prodotto delle sue diagonali (d ₁ d ₂ ) per il seno dell'angolo tra di loro:

S = ½ d ₁ d ₂ sin a.

Considera un'attività che mostra l'applicazione di questo metodo. Dato: un trapezio con una lunghezza di diagonali di 8 e 13 cm, rispettivamente. L'angolo a tra le diagonali è di 30 °. Trova l'area del trapezio.

La decisione Utilizzando la formula sopra, è facile calcolare il necessario. Come sai, peccato 30 ° è 0,5. Pertanto, S = 8 * 13 * 0,5 = 52. Risposta: l'area è di 52 metri quadrati. cm.

Stiamo cercando un'area di trapezio equilatero.

Un trapezio può essere equilatero (isoscele). I suoi lati sono uguali e gli angoli delle basi sono uguali, che è ben illustrato dal disegno. Un trapezio equilatero ha le stesse proprietà di uno normale, più un numero di speciali. Un cerchio può essere descritto attorno a un trapezio equipollico e in esso può essere inciso un cerchio.

Quali sono i metodi per calcolare l'area di una tale figura? Il seguente metodo richiederà grandi calcoli. Per usarlo, è necessario conoscere i valori seno (seno) e coseno (cos) dell'angolo alla base del trapezio. Per calcolarli, sono necessarie le tabelle Bradis o una calcolatrice tecnica. Ecco questa formula:

S = c * sin a * ( a - c * cos a ),

dove c è la coscia laterale, a è l'angolo nella base inferiore.

Un trapezio equilatero ha diagonali della stessa lunghezza. Il contrario è anche vero: se il trapezio diagonale è uguale, allora è isoscele. Quindi la seguente formula che aiuta a trovare l'area di un trapezio è il semiprodotto del quadrato delle diagonali al seno dell'angolo tra loro: S = ½ d ² sin a.

Trova l'area di un trapezio rettangolare

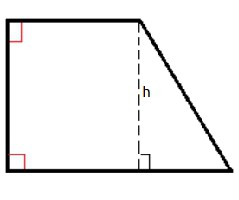
Caso speciale noto trapezio rettangolare. Questo è un trapezio, in cui un lato (la sua coscia) è adiacente alle basi ad angolo retto. Ha le proprietà di un trapezio ordinario. Inoltre, ha una caratteristica molto interessante. La differenza dei quadrati delle diagonali di un tale trapezio è uguale alla differenza dei quadrati delle sue basi. Per questo, usano tutti i metodi precedentemente descritti per il calcolo dell'area.

Applicare l'ingegno

C'è un trucco che può aiutare nel caso della dimenticanza di formule specifiche. Considera attentamente quale trapezio. Se lo dividiamo mentalmente in parti, diventeremo familiari e comprensibili forme geometriche: quadrato o rettangolo e triangolo (uno o due). Se l'altezza e i lati del trapezio sono noti, è possibile utilizzare le formule area del triangolo e un rettangolo, quindi sommare tutti i valori ottenuti.

Illustriamo questo con il seguente esempio. Dato un trapezio rettangolare. Angolo C = 45 °, angoli A, D sono 90 °. La base superiore del trapezio è di 20 cm, l'altezza è di 16 cm. È necessario calcolare l'area della figura.

decisione

Questa figura ovviamente consiste in un rettangolo (se i due angoli sono di 90 °) e un triangolo. Poiché il trapezio è rettangolare, quindi, la sua altezza è uguale al suo lato, cioè 16 cm. Abbiamo un rettangolo con lati di 20 e 16 cm, rispettivamente. Considera ora un triangolo il cui angolo è 45 °. Sappiamo che un lato di esso è di 16 cm. Dal momento che questo lato è allo stesso tempo l'altezza del trapezio (e sappiamo che l'altezza cade alla base ad angolo retto), quindi, il secondo angolo del triangolo è di 90 °. Quindi l'angolo rimanente del triangolo è 45 °. La conseguenza di ciò è che otteniamo un triangolo isoscele rettangolare, i cui due lati sono uguali. Ciò significa che l'altro lato del triangolo è uguale all'altezza, ovvero 16 cm. Resta da calcolare l'area del triangolo e del rettangolo e aggiungere i valori ottenuti.

zona triangolo rettangolo pari alla metà del prodotto delle sue gambe: S = (16 * 16) / 2 = 128. L'area del rettangolo è uguale al prodotto della sua larghezza per la lunghezza: S = 20 * 16 = 320. Abbiamo trovato l'area richiesta del trapezio S = 128 + 320 = 448 quadrati. Vedi. Puoi ricontrollare facilmente te stesso usando le formule sopra, la risposta sarà identica.

Usa la formula Scegli

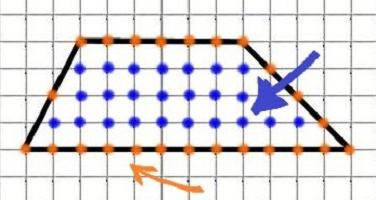
Infine, presentiamo un'altra formula originale che aiuta a trovare l'area di un trapezio. Si chiama la formula Pick. È conveniente usarlo quando il trapezio viene disegnato su carta a scacchi. Attività simili si trovano spesso nei materiali GIA. Sembra questo:

S = M / 2 + N - 1,

in questa formula, M è il numero di nodi, vale a dire l'intersezione delle linee della figura con le linee della cella ai bordi del trapezio (punti arancioni nella figura), N è il numero di nodi all'interno della figura (punti blu). È più comodo usarlo quando si trova l'area di un poligono irregolare. Tuttavia, maggiore è l'arsenale di metodi utilizzati, meno errori e migliori i risultati.

Naturalmente, le informazioni fornite sono lungi dall'essere esaurite dai tipi e dalle proprietà del trapezio, così come i metodi di ricerca della sua area. Questo articolo fornisce una panoramica delle sue caratteristiche più importanti. Nel risolvere problemi geometrici, è importante agire gradualmente, iniziare con formule e compiti facili, consolidare coerentemente la comprensione, passare a un altro livello di complessità.

Mettere insieme le formule più comuni aiuterà gli studenti ad orientarsi in vari modi di calcolare l'area di un trapezio e prepararsi meglio a test e test su questo argomento.