Quali difficoltà stanno aspettando coloro che si sono impegnati a eseguire l'aggiunta di radici?

Il tema delle radici quadrate è obbligatorio nel curriculum scolastico del corso di matematica. Senza di loro, non fare quando si decide equazioni quadrate. E più tardi diventa necessario non solo estrarre le radici, ma anche eseguire altre azioni con loro. Tra loro sono abbastanza complessi: elevamento a potenza moltiplicazione e divisione. Ma ci sono abbastanza semplici: sottrazione e aggiunta di radici. A proposito, sembrano solo così a prima vista. Eseguirli senza errori non è sempre facile per qualcuno che sta appena iniziando a conoscerli.

Qual è la radice matematica?

Questa azione ha avuto origine in opposizione all'esponenziazione. La matematica presuppone l'esistenza di due operazioni opposte. C'è sottrazione per l'aggiunta. La moltiplicazione è contrastata dalla divisione. L'inverso del grado è l'estrazione della radice corrispondente.

Se c'è un potere in due, allora la radice sarà quadrata. È più comune nella matematica scolastica. Non ha nemmeno l'indicazione che è quadrato, cioè il numero 2 non gli viene attribuito: la notazione matematica di questo operatore (radicale) è mostrata nella figura.

Dall'azione descritta segue senza problemi la sua definizione. Per estrarre radice quadrata da un certo numero, è necessario capire quale darà, quando si moltiplica in te stesso, l'espressione radicale. Questo numero sarà la radice quadrata. Se lo scrivi matematicamente, ottieni quanto segue: x * x = x ² = y, quindi √u = x.

Cosa puoi fare con loro?

Nel suo nucleo, la radice è un grado frazionale, in cui vi è un'unità nel numeratore. E il denominatore può essere qualsiasi. Ad esempio, nella radice quadrata, è uguale a due. Pertanto, tutte le azioni che possono essere eseguite con gradi saranno valide per le radici.

E i requisiti per queste azioni sono gli stessi. Se la moltiplicazione, la divisione e l'esponenziazione non incontrano difficoltà per gli studenti, l'aggiunta di radici, come la loro sottrazione, a volte porta a confusione. E tutto perché voglio eseguire queste operazioni senza riguardo al segno radice. E qui cominciano gli errori.

Quali sono le regole per aggiungerle e sottrarle?

Per prima cosa devi ricordare due categorici "no":

• non aggiungere e sottrarre radici, come numeri primi cioè, non è possibile scrivere espressioni radicali sommate single-sign ed eseguire operazioni matematiche con esse;
• non è possibile aggiungere e sottrarre radici con indicatori diversi, come quadrato e cubico.

Un buon esempio del primo divieto: √6 + √10 ≠ √16, ma √ (6 + 10) = √16 .

Nel secondo caso, è meglio limitarsi a semplificare le radici stesse. E nella risposta di lasciare la loro quantità.

Adesso alle regole

1. Trova e raggruppa radici simili. Cioè, quelli che hanno non solo gli stessi numeri sotto il radicale, ma loro stessi hanno lo stesso indicatore.
2. Per eseguire l'aggiunta delle radici, unite in un gruppo dalla prima azione. È facile da implementare, perché è sufficiente sommare i valori che stanno di fronte ai radicali.
3. Estrai le radici in quei termini in cui l'espressione radicale forma un intero quadrato. In altre parole, non lasciare nulla sotto il segno del radicale.
4. Semplifica l'espressione. Per fare ciò, è necessario scomporli in fattori primi e vedere se non daranno un quadrato di qualsiasi numero. È chiaro che questo è vero quando si tratta di radice quadrata. Quando l'esponente è tre o quattro, allora i fattori primi dovrebbero dare un cubo o la quarta potenza di un numero.
5. Rimuovere dal moltiplicatore di segno radicale, che dà l'intero grado.
6. Vedi se i termini simili appaiono di nuovo. In tal caso, quindi eseguire di nuovo la seconda azione.

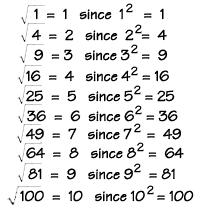
In una situazione in cui l'attività non richiede il valore esatto della radice, può essere calcolata sulla calcolatrice. Frazione decimale senza fine, che verrà visualizzata nella sua finestra, rotonda. Più spesso è fatto al centesimo. E quindi eseguire tutte le operazioni per frazioni decimali.

Raccomandazione: dopo la scomposizione in fattori primi, è necessario controllare. Vale a dire, moltiplicarli l'uno sull'altro e verificare se il valore originale è stato ottenuto.

Questa è tutta l'informazione su come viene eseguita l'aggiunta di radici. Gli esempi seguenti illustreranno quanto sopra.

Primo compito

Calcola il valore delle espressioni:

a) √2 + 3√32 + ½ √128 - 6√18;

b) √75 - √147 + √48 - 1/5 √300;

c) √275 - 10√11 + 2√99 + √396.

La decisione

a) Se segui l'algoritmo di cui sopra, è chiaro che per le prime due azioni in questo esempio non c'è nulla. Ma puoi semplificare alcune espressioni radicali.

Ad esempio, 32 è scomposto in due fattori 2 e 16; 18 sarà uguale al prodotto di 9 e 2; 128 è 2 per 64. Detto questo, l'espressione sarà scritta così:

√2 + 3√ (2 * 16) + ½ √ (2 * 64) - 6 √ (2 * 9).

Ora dobbiamo rimuovere dal segno radicale quei fattori che danno il quadrato di un numero. Questo è 16 = 4 ² , 9 = 3 ² , 64 = 8 ² . L'espressione sarà simile a:

√2 + 3 * 4√2 + ½ * 8 √2 - 6 * 3√2.

Hai bisogno di un po 'più facile da scrivere. Per fare questo, moltiplica i coefficienti di fronte ai segni della radice:

√2 + 12√2 + 4 √2 - 12√2.

In questa espressione, tutti i termini si sono rivelati simili. Pertanto, hanno solo bisogno di piegare. La risposta sarà: 5√2.

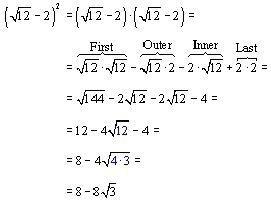
b) Come nell'esempio precedente, l'aggiunta delle radici inizia con la loro semplificazione. Le espressioni radicali 75, 147, 48 e 300 saranno rappresentate dalle seguenti coppie: 5 e 25, 3 e 49, 3 e 16, 3 e 100. Ciascuno di essi ha un numero che può essere rimosso dal segno radice:

5√5 - 7√3 + 4√3 - 1/5 * 10√3.

Dopo la semplificazione, otteniamo la risposta: 5√5 - 5√3. Può essere lasciato in questa forma, ma è meglio prendere il fattore 5 comune per la parentesi: 5 (√5 - √3).

c) E ancora, factoring: 275 = 11 * 25, 99 = 11 * 9, 396 = 11 * 36. Dopo aver rimosso i fattori dal segno radice, otteniamo:

5√11 - 10√11 + 2 * 3√11 + 6√11. Dopo aver introdotto tali termini, otteniamo il risultato: 7√11.

Esempio con espressioni frazionarie

√ (45/4) - √20 - 5√ (1/18) - 1/6 √245 + √ (49/2).

I fattori dovranno decomporre i seguenti numeri: 45 = 5 * 9, 20 = 4 * 5, 18 = 2 * 9, 245 = 5 * 49. Simile a quelli già considerati, è necessario rimuovere i fattori dal segno radice e semplificare l'espressione:

3/2 √5 - 2√5 - 5/3 √ (½) - 7/6 √5 + 7 √ (½) = (3/2 - 2 - 7/6) √5 - (5/3 - 7 ) √ (½) = - 5/3 √5 + 16/3 √ (½).

Questa espressione richiede di liberarsi dell'irrazionalità nel denominatore. Per fare ciò, moltiplicare per √2 / √2 il secondo termine:

- 5/3 √5 + 16/3 √ (½) * √2 / √2 = - 5/3 √5 + 8/3 √2.

Per completezza dell'azione, è necessario selezionare la parte intera dei fattori prima delle radici. Nel primo, è uguale a 1, nel secondo - 2.