Cos'è una striscia di Möbius? Striscia di Mòbius: il mistero del nostro tempo

Ci sono conoscenze scientifiche e fenomeni che portano mistero e mistero alla routine quotidiana delle nostre vite. Ribbon Moebius si riferisce a loro completamente. La matematica moderna descrive perfettamente tutte le sue proprietà e caratteristiche usando le formule. Ma la gente comune, scarsamente versata nella toponomastica e in altre saggezze geometriche, quasi ogni giorno si confronta con oggetti fatti a sua immagine e somiglianza, senza nemmeno saperlo.

Cos'è?

La striscia di Möbius, chiamata anche loop, superficie o foglio, è l'oggetto di studio di una tale disciplina matematica come topologia, che esplora le proprietà generali delle forme che vengono conservate in tali trasformazioni continue come torsioni, stiramenti, compressione, piegature e altre non correlate alla violazione dell'integrità. . Una caratteristica sorprendente e unica di un tale nastro è che ha solo un lato e un bordo e non è in alcun modo connessa con la sua posizione nello spazio. La striscia di Möbius è un topologico, cioè un oggetto continuo con la superficie unilaterale più semplice con un bordo nel consueto spazio euclideo (tridimensionale), dove è possibile raggiungere qualsiasi altro da un punto di tale superficie senza attraversare i bordi.

Chi l'ha aperto e quando?

Un oggetto così a disagio come la striscia di Möbius era ed è aperto piuttosto inusuale. Prima di tutto, notiamo che due matematici, totalmente estranei l'uno all'altro nella ricerca, lo scoprirono simultaneamente - nel 1858. Un altro fatto interessante è che entrambi questi scienziati in tempi diversi erano studenti dello stesso grande matematico: Johann Karl Friedrich Gauss. Quindi, fino al 1858 si credeva che ogni superficie dovesse avere due lati. Tuttavia, Johann Benedict Listing e August Ferdinand Mobius scoprirono un oggetto geometrico che aveva solo un lato e ne descrivevano le proprietà. Il nastro prende il nome da Mobius, ma i topologi considerano Listing e il suo lavoro "Studi preliminari sulla topologia" come padre fondatore della "geometria della gomma".

proprietà

La striscia di Möbius ha le seguenti proprietà che non cambiano quando vengono spremute, tagliate o schiacciate:

1. La presenza di un lato A. Mobius nella sua opera "Sul volume dei poliedri" descrive una superficie geometrica, che prende il nome da lui, che ha un solo lato. È abbastanza semplice controllare: prendiamo un nastro o una striscia di Möbius e proviamo a dipingere l'interno con un colore e l'esterno con un altro. Non importa in quale luogo e direzione è stata avviata la colorazione, l'intera figura verrà dipinta con un solo colore.

2. La continuità è espressa nel fatto che qualsiasi punto di questo forma geometrica Puoi collegarlo a qualsiasi altro punto senza oltrepassare i limiti della superficie di Mobius.

3. La connettività, o bidimensionalità, sta nel fatto che durante il taglio del nastro, molte forme diverse non ne usciranno e rimarranno integre.

4. Manca una proprietà così importante come orientamento. Ciò significa che una persona che cammina su questa figura tornerà all'inizio del suo percorso, ma solo nello specchio riflesso di se stesso. Quindi, il nastro infinito di Möbius può portare al viaggio eterno.

5. Un numero cromatico speciale che indica il numero massimo possibile di aree sulla superficie di Mobius in modo che ciascuna di esse abbia un bordo comune con tutte le altre. La striscia di Mobius ha un numero cromatico - 6, ma un anello di carta è 5.

Uso scientifico

Oggi, la striscia di Möbius e le sue proprietà sono ampiamente utilizzate nella scienza, servendo come base per la costruzione di nuove ipotesi e teorie, conducendo ricerche ed esperimenti, creando nuovi meccanismi e dispositivi.

Quindi, c'è un'ipotesi che l'universo sia un enorme anello di Mobius. Testimonia indirettamente a questo e La teoria della relatività di Einstein, secondo cui persino una nave che è volata direttamente può ritornare allo stesso punto temporale e spaziale da cui è partita.

Un'altra teoria considera il DNA come parte della superficie di Möbius, il che spiega la difficoltà di lettura e decodifica codice genetico. Tra le altre cose, questa struttura fornisce una spiegazione logica per la morte biologica - la spirale chiusa su se stessa porta all'autodistruzione dell'oggetto.

Secondo i fisici, molte leggi ottiche si basano sulle proprietà della striscia di Möbius. Quindi per esempio immagine speculare - Questo è un trasferimento speciale nel tempo e una persona vede la sua controparte speculare di fronte a lui.

Implementazione nella pratica

In vari settori, la striscia di Mobius ha trovato un'applicazione per molto tempo. Grande inventore Nikola Tesla all'inizio del secolo ha inventato il resistore di Möbius, costituito da due superfici conduttive ritorte da 180 ⁰ , in grado di resistere al flusso di corrente elettrica senza creare interferenze elettromagnetiche.

Sulla base di studi sulla superficie della striscia di Möbius e delle sue proprietà, sono stati creati molti dispositivi e dispositivi. La sua forma viene ripetuta quando si crea una striscia di nastro trasportatore e nastro inchiostrato in dispositivi di stampa, nastri abrasivi per strumenti di affilatura e trasferimento automatico. Ciò consente di aumentare significativamente la durata in servizio, poiché l'usura si verifica in modo più uniforme.

Non molto tempo fa, le straordinarie caratteristiche della striscia di Möbius hanno permesso di creare una molla, che, a differenza di quelle ordinarie che operano nella direzione opposta, non modifica la direzione di funzionamento. Viene utilizzato nello stabilizzatore dello sterzo del volante, garantendo il ritorno del volante nella posizione originale.

Inoltre, il badge della striscia Mobius viene utilizzato in vari marchi e loghi. Il più famoso di loro è il simbolo internazionale del riciclaggio. È apposto sull'imballaggio di merci o adatto per ulteriori elaborazioni o fatto con risorse riciclate.

Fonte di ispirazione creativa

La striscia di Möbius e le sue proprietà hanno costituito la base per il lavoro di molti artisti, scrittori, scultori e cineasti. L'artista più famoso che ha usato in opere come "Il nastro di Moebius II (Red Ants)", "The Riders" e "Knots", il nastro e le sue caratteristiche è Maurits Cornelis Escher.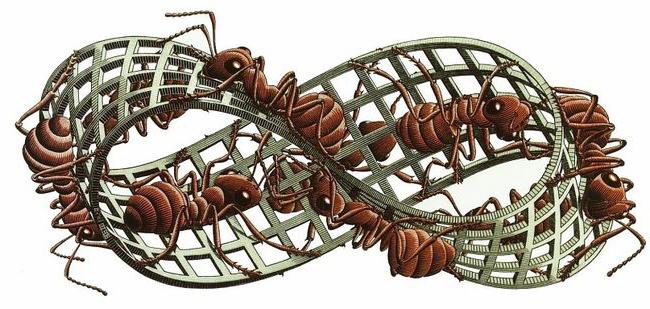

I fogli di Moebius, o, come vengono anche chiamati, le superfici di energia minima, divennero una fonte di ispirazione per artisti e scultori matematici, per esempio, Brent Collins o Max Bill. Il monumento più famoso della striscia Mobius è installato all'ingresso del Museo di Storia e Tecnologia di Washington.

Anche gli artisti russi non sono stati lontani da questo argomento e hanno creato le loro opere. Sculture "Ribbon Moebius" installate a Mosca e Ekaterinburg.

Letteratura e topologia

Le proprietà insolite delle superfici di Moebius hanno ispirato molti scrittori a creare opere fantastiche e surreali. Il loop di Mobius gioca un ruolo importante nel romanzo "Doors in the Sand" di R. Zelazny e serve come mezzo per muoversi nello spazio e nel tempo per il personaggio principale del romanzo "The Necroscope" B. Lumley.

Appare anche nelle storie The Wall of Darkness di Arthur Clarke, Sul nastro di Mobius di M. Clifton e The Mobius Sheet di A.J. Deutsch. Sulla base dell'ultimo regista Gustavo Mosquera è stato girato un film fantastico "Mobius".

Fai da te, con le tue mani!

Se sei interessato alla striscia di Möbius, come farne un modello, ti verrà richiesto da una piccola istruzione:

1. Per la fabbricazione del suo modello richiederà:

- un foglio di carta comune;

- forbici;

- linea.

2. Taglia la striscia dal foglio di carta in modo che la sua larghezza sia 5-6 volte inferiore alla lunghezza.

3. La striscia di carta risultante su una superficie piana. Tenere un'estremità con la mano e ruotare l'altra estremità di 180 ^{° in} modo che la striscia sia attorcigliata e il lato sbagliato diventi il ​​lato anteriore.

4. Incolliamo le estremità della striscia attorcigliata come mostrato nella figura. 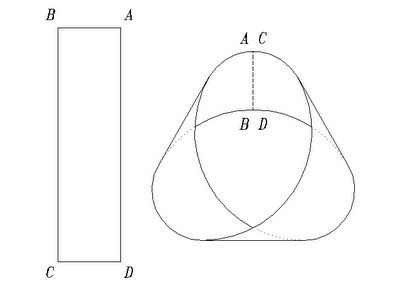Il nastro di Mobius è pronto.

5. Prendi una penna o un pennarello e inizia a disegnare un tracciato nel mezzo del nastro. Se hai fatto tutto correttamente, tornerai allo stesso punto dal quale hai iniziato a tracciare una linea.

Per ottenere una conferma visiva che la striscia di Möbius è un oggetto a parte, prova a dipingere su qualsiasi lato con una matita o una penna. Dopo un po 'vedrai che lo hai dipinto completamente.