Cos'è la gravità e qual è il suo significato per la vita sulla Terra

Il diciassettesimo secolo non è senza ragione chiamato il secolo delle grandi scoperte astronomiche. Le osservazioni a lungo termine di Galileo, Copernico e Tycho Brahe hanno permesso a Johann Kepler di formare le leggi del moto dei corpi celesti. Per spiegare perché i pianeti sono in movimento infinito, cosa li fa rimanere nella loro orbita, e cos'è la gravità, ci vuole un genio: Isaac Newton.

Genio di ipotesi

Isaac Newton formulò le sue leggi sul movimento non per la teoria, ma per l'applicazione pratica. Riassumendo i dati di osservazioni astronomiche perenni e grazie alle sue leggi del moto, questo grande scienziato è stato in grado di rispondere a una domanda che ha confuso più di una generazione di scienziati: "Cosa tiene i pianeti nelle loro orbite?" Infatti, prima di Newton, gli scienziati propongono varie ipotesi - dalle sfere di cristallo alle fluidi magnetici. grazie La prima legge di Newton divenne chiaro che la forza non era necessaria per un moto rettilineo uniforme. La forza è necessaria per far muovere i pianeti in un'orbita curvilinea. Se applichiamo la formula della forza dalla seconda legge di Newton, allora sarà uguale al prodotto dell'accelerazione per massa. Newton arrivò alla conclusione che l'accelerazione doveva essere uguale a v ² / R. Quindi un corpo celeste più leggero, per esempio, la Luna ruoterà attorno a un più pesante, ma non si avvicinerà mai a esso. Questo può essere pensato come cadendo da una tangente a un cerchio sul cerchio stesso. Al punto di contatto la velocità può essere costante o uguale a zero, ma l'accelerazione è sempre presente. Movimento costante in una data orbita senza l'assenza di accelerazione visibile - questa è la risposta di Newton alla domanda sul moto dei pianeti.

attrazione

Quindi, la Luna si muove attorno alla Terra e alla Terra, attorno al Sole, obbedendo a una certa forza. Il genio di Newton si manifestò nel fatto che egli combinò la forza gravitazionale dei corpi celesti con la gravità, che è nota ad ogni abitante della Terra. C'è una leggenda secondo cui una mela normale che gli cadeva sulla testa veniva spinta alle giuste conclusioni di Newton. L'attrazione della mela e della luna sulla Terra è descritta secondo leggi assolutamente identiche - conclude il ricercatore. Gravity ha ricevuto il suo secondo nome dalla parola "gravis", che significa "peso".

gravitazione

Riassumendo le leggi del moto dei pianeti, Newton ha scoperto che la forza della loro interazione può essere calcolata con la formula: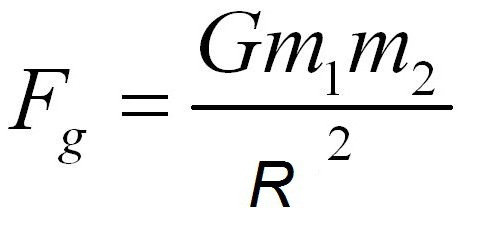

Dove m ₁ m ₂ sono le masse dei corpi interagenti, R è la distanza tra loro, e G è un certo coefficiente di proporzionalità, chiamato costante gravitazionale. La parola "gravità" viene scelta in modo assolutamente corretto, perché deriva dalla parola "peso". Il numero esatto del costante Newton non era noto, molto più tardi il valore di G stabilì il Cavendish. Si può vedere che l'azione della forza di attrazione è influenzata dalle masse dei corpi e la distanza tra loro è presa in considerazione. Nessun altro fattore può influenzare la forza di gravità.

Significato della legge di attrazione

Questa legge è universale e può essere applicata a qualsiasi due corpi che hanno una massa. Nel caso in cui la massa di un corpo interagente sia molto più grande della massa dell'altro, possiamo parlare di un caso particolare di forza gravitazionale, per il quale esiste un termine speciale "gravità". Questo concetto è usato per problemi che calcolano la forza di gravità sulla Terra o altri corpi celesti. Se sostituiamo il valore della gravità nella formula della seconda legge di Newton, otteniamo il valore F = ma. Qui a è l'accelerazione della gravità, che fa sì che il corpo si sforzi l'uno verso l'altro. Nei compiti associati all'uso di accelerazione gravitazionale di solito è indicato con la lettera g. Con l'aiuto del calcolo integrale sviluppato da lui, Newton ha dimostrato matematicamente che la forza di gravità in una palla è sempre concentrata nel centro di un corpo più grande. Nella coppia terra-mela, il vettore di accelerazione è diretto verso il centro della terra, nella coppia terra-sole è diretto verso il sole e così via.

Dipendenza dalla gravità sulla latitudine

La gravità sulla Terra dipende dall'altezza del corpo al di sotto della superficie del pianeta e dalla latitudine in cui viene condotto l'esperimento. L'altezza del corpo influisce sul valore di R, come si può vedere, più lontana è la distanza dalla superficie della Terra, minore è il valore di g. La connessione della gravità con la latitudine è spiegata dal fatto che la Terra ha la forma di un geoide, non di una sfera. Ai poli, è un po 'schiacciato. Pertanto, la distanza dal centro della Terra all'equatore e al polo sarà diversa, fino al 10%. Tale discrepanza rende piuttosto scomodi i calcoli, ad esempio i calcoli dei trasporti transcontinentali di merci. Pertanto, l'indicatore si basa sulla forza di attrazione a medie latitudini di 9,81 m / s ² .

Peso corporeo

Nella vita di tutti i giorni è ampiamente usato qualcosa come il peso corporeo. In fisica, è indicato dalla lettera P. Il peso è la forza con cui il corpo preme contro il supporto. Nel concetto domestico di peso viene spesso sostituito dal concetto di "massa", sebbene questi siano valori completamente diversi. A seconda del valore che assume la gravità, cambia anche il peso del corpo. Ad esempio, il peso della parte guida sulla Terra e sulla Luna sarà diverso. Ma la massa rimane invariata sia sulla Terra che sulla Luna. Inoltre, in alcuni casi, il peso corporeo può essere zero. Il peso è un valore che ha direzione e la massa è uno scalare.

Ma poiché, secondo la terza legge di Newton, l'azione è uguale all'opposizione, il peso del corpo è uguale alla forza della reazione di sostegno.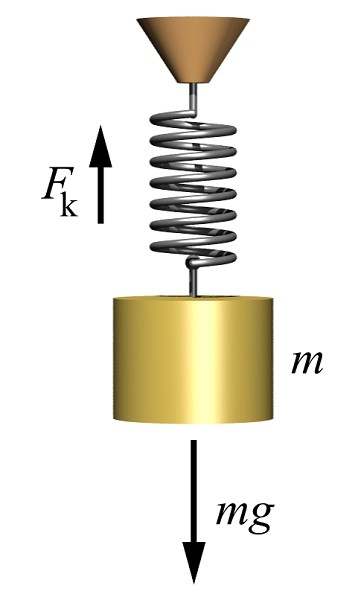

Poiché la forza di reazione di un semplice supporto è piuttosto difficile da misurare, l'esperienza può essere "capovolta" appendendo un corpo a una molla e misurando il grado di stiramento di questa primavera. In questo caso, la forza che estende la molla con il carico avrà un F = mg completamente logico, dove m è la massa e g è l'accelerazione di gravità.

sovraccarico

Se il carico con la molla viene sollevato, l'accelerazione della gravità e l'accelerazione dell'ascensore saranno dirette in direzioni opposte. Questo può essere rappresentato come segue: F = m (g + a). La gravità, e di conseguenza, e il suo peso, aumentano.

Per aumentare il peso associato all'accelerazione aggiuntiva, c'è un termine speciale: sovraccarico. L'effetto del sovraccarico è stato sperimentato da ognuno di noi, prendendo l'ascensore o decollando su un aereo. I cosmonauti e i piloti di velivoli supersonici provano un sovraccarico particolarmente pesante quando prendono il loro aereo.

assenza di gravità

Quando al corpo viene data accelerazione nella direzione della gravità, cioè nel nostro caso, quindi F = m (ga). Quindi, il peso corporeo diventa meno. Nel caso limite, quando a = ge sono diretti in direzioni diverse, si può parlare di peso zero, cioè il corpo cade a velocità costante. Una condizione in cui il peso corporeo è zero è chiamata assenza di peso. Una persona sperimenta uno stato di gravità zero in un'astronave quando si muove con i motori spenti. L'assenza di gravità è una condizione comune per gli astronauti e i piloti che volano su aeroplani supersonici.

Valore di gravità

Senza gravità, non ci sarebbero molte cose che a noi sembrano naturali, le cose non andrebbero giù come una valanga dalle montagne, non pioverebbero, i fiumi non fluiranno. L'atmosfera terrestre è preservata dalla gravità. Per fare un confronto, i pianeti con una massa più piccola, come la Luna o Mercurio, hanno perso la loro atmosfera molto rapidamente e sono rimasti senza difese contro il flusso di radiazioni cosmiche dure. L'atmosfera della Terra ha svolto un ruolo cruciale nell'emergere della vita sulla Terra, nella sua modifica e conservazione.

Oltre alla gravità, la forza di gravità della Luna agisce sulla Terra. Grazie al suo vicino (su scala cosmica) quartiere sulla Terra, ci sono flussi e riflussi, i continenti si spostano e molti ritmi biologici coincide con il calendario lunare.

Quindi, la gravità deve essere vista non come un fastidioso ostacolo, ma come una legge utile e necessaria della natura.