Cosa è il seno e il coseno nella trigonometria?

Gli insegnanti credono che ogni scolaro dovrebbe essere in grado di eseguire calcoli, conoscere le formule trigonometriche, ma non tutti gli insegnanti spiegano cosa sono seno e coseno. Qual è il loro significato, dove vengono utilizzati? Perché stiamo parlando di triangoli e nel libro di testo è disegnato un cerchio? Proviamo a legare insieme tutti i fatti.

Materia scolastica

Lo studio della trigonometria di solito inizia nel grado 7-8. In questo momento, agli studenti viene detto che sono seno e coseno, si propongono di risolvere problemi geometrici usando queste funzioni. Più tardi appaiono formule e espressioni più complesse che devono essere trasformate in modo algebrico (formule di doppio e semiangolo, funzioni di potere) e il lavoro viene eseguito con un cerchio trigonometrico.

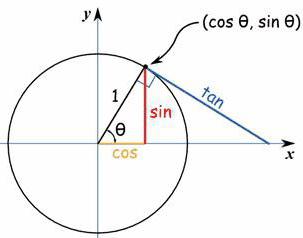Tuttavia, gli insegnanti non sono sempre in grado di spiegare chiaramente il significato dei concetti utilizzati e l'applicabilità delle formule. Pertanto, lo studente spesso non vede il punto in questo argomento e le informazioni memorizzate vengono rapidamente dimenticate. Tuttavia, vale la pena di spiegare una volta ad uno studente liceale, ad esempio, la connessione tra funzione e movimento oscillatorio, e la connessione logica sarà ricordata per molti anni, e le battute sull'inutilità del soggetto saranno una cosa del passato.

Uso di

Cerchiamo la curiosità in varie sezioni della fisica. Vuoi determinare la portata del proiettile? O calcolare la forza di attrito tra un oggetto e una certa superficie? Dondolando il pendolo, osservando i raggi che passano attraverso il vetro, calcola l'induzione? Praticamente in qualsiasi formula compaiono concetti trigonometrici. Quindi cos'è il seno e il coseno?

definire

Il seno dell'angolo è il rapporto tra la gamba opposta e l'ipotenusa, il coseno della gamba adiacente è lo stesso della stessa ipotenusa. Non c'è assolutamente nulla di complicato. Forse gli studenti sono generalmente confusi dai valori che vedono nella tabella trigonometrica, perché appaiono radici quadrate. Sì, esci da loro decimali non molto conveniente, ma chi ha detto che tutti i numeri in matematica dovrebbero essere pari?

In effetti, puoi trovare un suggerimento divertente nei libri di problemi della trigonometria: la maggior parte delle risposte qui sono pari e nel peggiore dei casi contengono la radice di due o tre. La conclusione è semplice: se si ottiene una frazione "a più piani" nella risposta, ricontrollare la decisione relativa agli errori nei calcoli o negli argomenti. E molto probabilmente li troverai.

Quello che devi ricordare

Come in ogni scienza, nella trigonometria ci sono dati che devono essere appresi.

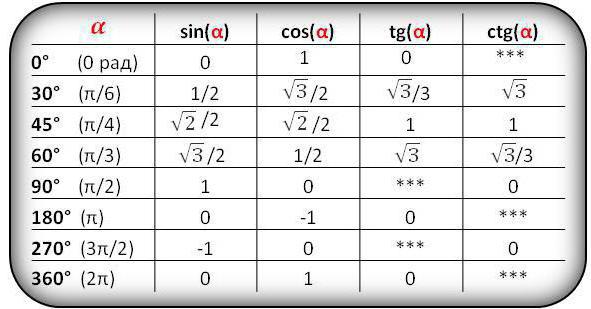
Per prima cosa, ricorda i valori numerici per seni, coseni triangolo rettangolo 0 e 90, nonché 30, 45 e 60 gradi. Questi indicatori si trovano in nove compiti scolastici su dieci. Sbirciando questi valori nel libro di testo, perderai molto tempo e non ci sarà posto per esaminare il test o l'esame.

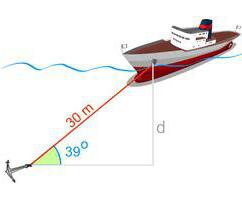È necessario ricordare che il valore di entrambe le funzioni non può essere superiore a uno. Se da qualche parte nei calcoli ottieni un valore al di fuori dell'intervallo 0-1, fermati e risolvi il problema.

La somma dei quadrati di seno e coseno è uguale a uno. Se hai già trovato uno dei valori, usa questa formula per trovare il rimanente.

teorema

Nella trigonometria di base, ci sono due teoremi principali: seni e coseni.

Il primo dice che il rapporto tra ciascun lato del triangolo e il seno dell'angolo opposto è lo stesso. Il secondo è che il quadrato di qualsiasi lato può essere ottenuto aggiungendo i quadrati dei due lati rimanenti e sottraendo il loro prodotto raddoppiato moltiplicato per il coseno dell'angolo tra loro.

Quindi, se in teorema del coseno Sostituisci il valore dell'angolo di 90 gradi, otteniamo ... il teorema di Pitagora. Ora, se vuoi calcolare l'area di una figura che non è un triangolo rettangolo, non puoi più preoccuparti - i due teoremi considerati semplificheranno significativamente la soluzione del problema.

Obiettivi e obiettivi

Studiare la trigonometria sarà enormemente semplificata quando realizzerete un semplice fatto: tutte le azioni che eseguite mirano a raggiungere un solo obiettivo. Qualsiasi parametro di un triangolo può essere trovato se si conoscono le informazioni minime su di esso - può essere il valore di un angolo e la lunghezza di due lati o, ad esempio, di tre lati.

Per determinare il seno, il coseno, la tangente di qualsiasi angolo di questi dati è sufficiente, con il loro aiuto, è possibile calcolare facilmente l'area della figura. Quasi sempre, uno dei valori menzionati è richiesto come risposta, e possono essere trovati usando le stesse formule.

Incoerenze nello studio della trigonometria

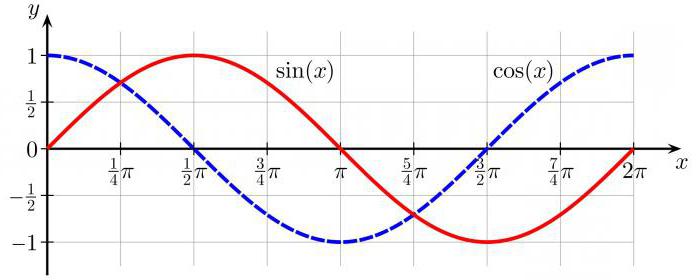
Una delle domande oscure che gli studenti preferiscono evitare è trovare la connessione tra i diversi concetti in trigonometria. Sembrerebbe che i triangoli siano usati per studiare i seni e il coseno degli angoli, ma per qualche motivo, i simboli si trovano spesso nella figura con un cerchio. Inoltre, c'è un grafico a forma d'onda incomprensibile chiamato sinusoide, che non ha alcuna somiglianza esterna con un cerchio o un triangolo.

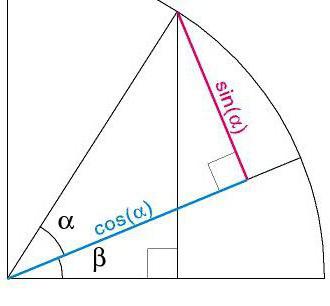Inoltre, gli angoli sono misurati in gradi, quindi in radianti, e il numero Pi, scritto semplicemente come 3.14 (senza unità), per qualche ragione appare nelle formule, corrispondenti a 180 gradi. In che modo tutto questo è in relazione tra loro?

Unità di misura

Perché p pi esattamente 3,14? Ti ricordi cos'è questo valore? Questo è il numero di raggi che si adattano in un arco a semicerchio. Se il diametro del cerchio è 2 centimetri, circonferenza sarà 3,14 * 2, o 6,28.

Il secondo punto: potresti aver notato la somiglianza tra "radian" e "radius". Il fatto è che un radiante è numericamente uguale all'angolo tra il centro del cerchio e l'arco con una lunghezza di un raggio.

Ora combiniamo le conoscenze ottenute e comprendiamo perché la parola "Pi a metà" è scritta sull'asse delle coordinate in trigonometria e sulla sinistra - "Pi". Questo è un valore angolare, misurato in radianti, perché un semicerchio è di 180 gradi o 3,14 radianti. E dove ci sono gradi, ci sono seni e coseni. Il triangolo è facile da tenere dal punto desiderato, mettendo i segmenti al centro e sull'asse delle coordinate.

Guarda nel futuro

La trigonometria, studiata a scuola, si occupa di un sistema di coordinate rettilineo, in cui, per quanto strano possa sembrare, una linea retta è una linea retta.

Ma ci sono modi più complessi di lavorare con lo spazio: la somma degli angoli di un triangolo qui sarà più di 180 gradi, e la linea nella nostra vista sembrerà un vero arco.

Passiamo dalle parole ai fatti! Prendi una mela. Fai tre incisioni con un coltello in modo che, visto da sopra, ottieni un triangolo. Estrarre il pezzo di mela risultante e guardare le "costole" dove termina la crosta. Non sono affatto diretti. Il frutto nelle tue mani può essere definito un round, e ora immagina quanto dovrebbero essere complesse le formule con le quali puoi trovare l'area del pezzo tagliato. Ma alcuni esperti risolvono quotidianamente tali problemi.

Funzioni trigonometriche nella vita

Avete notato che il percorso più breve del velivolo dal punto A al punto B sulla superficie del nostro pianeta ha una forma di arco pronunciata? La ragione è semplice: la terra ha la forma di una sfera, il che significa che non puoi calcolare molto con l'aiuto dei triangoli - qui devi usare formule più complesse

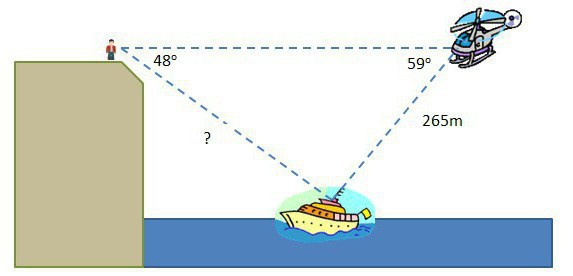
Non fare a meno del seno / coseno di un angolo acuto in tutte le questioni legate allo spazio. È interessante notare che qui convergono una moltitudine di fattori: le funzioni trigonometriche sono necessarie quando si calcola il moto dei pianeti in cerchi, ellissi e varie traiettorie di forme più complesse; il processo di lancio di razzi, satelliti, navette, disancoraggio di apparati di ricerca; osservare stelle lontane e studiare galassie che l'uomo non può raggiungere nel prossimo futuro.

In generale, il campo per l'attività umana, che possiede la trigonometria, è molto ampio e, a quanto pare, si espanderà solo nel tempo.

conclusione

Oggi abbiamo imparato o, in ogni caso, ripetuto cosa sono seno e coseno. Questi sono concetti che non hanno bisogno di avere paura - dovresti, e capirai il loro significato. Ricorda che la trigonometria non è un obiettivo, ma solo uno strumento che può essere utilizzato per soddisfare i reali bisogni umani: costruire case, fornire sicurezza del traffico, persino esplorare gli spazi aperti dell'universo.

In effetti, la scienza stessa può sembrare noiosa, ma una volta che trovi in ​​esso un modo per raggiungere i tuoi obiettivi, l'autorealizzazione, il processo di apprendimento diventerà interessante e la tua motivazione personale aumenterà.

Come compito a casa, cerca di trovare modi per applicare funzioni trigonometriche nell'area di attività che ti interessano personalmente. Immagina, accendi l'immaginazione, e poi scoprirai sicuramente che le nuove conoscenze ti saranno utili in futuro. Inoltre, la matematica è utile per lo sviluppo generale del pensiero.