Divisione per zero. Matematica affascinante

Il numero 0 può essere rappresentato come una sorta di confine che separa il mondo dei numeri reali da quelli immaginari o negativi. A causa della posizione ambigua, molte operazioni con questo valore numerico non sono soggette alla logica matematica. L'impossibilità di dividere per zero è un chiaro esempio. E le operazioni aritmetiche risolte con zero possono essere eseguite utilizzando le definizioni generalmente accettate.

Storia di zero

Zero è un punto di riferimento in tutti i sistemi di calcolo standard. Gli europei hanno iniziato a usare questo numero relativamente di recente, ma i saggi India antica usato zero per mille anni prima che il numero vuoto fosse usato regolarmente dai matematici europei. Anche prima degli indiani, lo zero era una quantità obbligatoria nel sistema numerico maya. Questo popolo americano usava il calcolo duodenale e con zero iniziarono il primo giorno di ogni mese. È interessante notare che in Maya il segno che indica "zero" coincide completamente con il segno che definisce "infinito". Quindi, l'antica Maya concluse che queste quantità sono identiche e inconoscibili.

Operazioni matematiche con zero

Le operazioni matematiche standard con zero possono essere ridotte a diverse regole.

Aggiunta: se zero viene aggiunto a un numero arbitrario, non cambierà il suo valore (0 + x = x).

Sottrazione: quando sottrarre zero da qualsiasi numero, il valore della sottrazione rimane invariato (x-0 = x).

Moltiplicazione: qualsiasi numero moltiplicato per 0 dà 0 nel prodotto (a * 0 = 0).

Divisione: zero può essere diviso per qualsiasi numero che non è uguale a zero. In questo caso, il valore di tale frazione è 0. E la divisione per zero è proibita.

Elevamento a potenza. Questa azione può essere eseguita con qualsiasi numero. Un numero arbitrario innalzato al grado zero darà 1 (x ⁰ = 1).

Lo zero è 0 a qualsiasi grado (0 ^a = 0).

In questo caso, immediatamente sorge una contraddizione: l'espressione 0 ⁰ non ha senso.

Paradossi della matematica

Il fatto che la divisione per zero sia impossibile, molti lo sanno da scuola. Ma per qualche ragione è impossibile spiegare la ragione di tale divieto. Infatti, perché la formula per la divisione per zero non esiste, ma altre azioni con questo numero sono abbastanza ragionevoli e possibili? La risposta a questa domanda è data dai matematici.

Il fatto è che le solite operazioni aritmetiche che gli alunni studiano nella scuola elementare sono di fatto lontane dall'essere uguali nei diritti, come ci sembra. Tutte le operazioni semplici con i numeri possono essere ridotte a due: addizione e moltiplicazione. Queste azioni costituiscono l'essenza del concetto stesso di un numero, mentre le restanti operazioni si basano sull'uso di questi due.

Addizione e moltiplicazione

Prendi l'esempio di sottrazione standard: 10-2 = 8. A scuola, è considerato semplicemente: se due articoli sono presi da dieci articoli, otto rimarranno. Ma i matematici considerano questa operazione in modo abbastanza diverso. Dopotutto, una tale operazione come sottrazione non esiste per loro. Questo esempio può essere scritto in un altro modo: x + 2 = 10. Per i matematici, la differenza sconosciuta è solo un numero che deve essere aggiunto a due per fare otto. E non è necessaria alcuna sottrazione qui, devi solo trovare il valore numerico appropriato.

Moltiplicazione e divisione sono considerati uguali. Nell'esempio 12: 4 = 3, si può capire che si tratta di dividere otto oggetti in due gruppi uguali. Ma in realtà, questa è solo una formula invertita del record 3x4 = 12. Tali esempi di divisione possono essere dati all'infinito.

Esempi di divisione per 0

Qui diventa un po 'chiaro perché è impossibile dividere per zero. La moltiplicazione e la divisione per zero obbediscono alle sue stesse regole. Tutti gli esempi della divisione di questa quantità possono essere formulati come 6: 0 = x. Ma questo è un record invertito dell'espressione 6 * x = 0. Ma, come sapete, qualsiasi numero moltiplicato per 0 dà solo 0 nel prodotto: questa proprietà è inerente al concetto stesso di valore zero.

Si scopre che non esiste un numero tale che, moltiplicato per 0, fornisca alcun valore tangibile, cioè questo compito non ha soluzione. Questa risposta non dovrebbe essere temuta, è una risposta naturale per compiti di questo tipo. Scrivere solo 6: 0 non ha senso, e lei non può spiegare nulla. In breve, questa espressione può essere spiegata dalla immortale "divisione per zero è impossibile".

Esiste un'operazione 0: 0? Infatti, se l'operazione di moltiplicazione per 0 è legale, può essere divisa zero per zero? Dopo tutto, un'equazione della forma 0x 5 = 0 è completamente legale. Invece del numero 5, puoi mettere 0, il prodotto di questo non cambierà.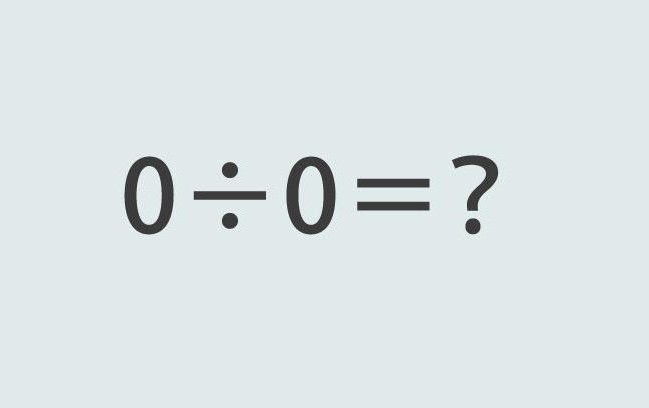

Anzi, 0x0 = 0. Ma è ancora impossibile dividere per 0. Come accennato, la divisione è semplicemente la moltiplicazione inversa. Quindi, se nell'esempio 0x5 = 0, dobbiamo determinare il secondo fattore, otteniamo 0x0 = 5. O 10. O infinito. Dividendo l'infinito per zero - come ti piace?

Ma se qualsiasi numero si adatta all'espressione, allora non ha senso, non possiamo sceglierne uno da un insieme infinito di numeri. E se è così, significa che l'espressione 0: 0 non ha senso. Si scopre che nemmeno lo zero stesso può essere diviso per zero.

Matematica superiore

Dividere per zero è un mal di testa per la matematica scolastica. Studiato in università tecniche analisi matematica espande leggermente il concetto di attività che non hanno soluzione. Ad esempio, per l'espressione già nota 0: 0 ne vengono aggiunti di nuovi che non hanno soluzione nei corsi di matematica scolastica:

• infinito diviso per l'infinito: ∞: ∞;
• infinito meno infinito: ∞ - ∞;
• unità elevata a potenza infinita: 1 ^∞ ;
• infinito moltiplicato per 0: ∞ * 0;
• alcuni altri.

I metodi elementari per risolvere tali espressioni sono impossibili. Ma la matematica più elevata, a causa di ulteriori possibilità per un numero di esempi simili, fornisce soluzioni finali. Ciò è particolarmente evidente nella considerazione dei problemi dalla teoria dei limiti.

Divulgazione dell'incertezza

Nella teoria dei limiti, il valore 0 è sostituito da una variabile condizionale infinitamente piccola. E le espressioni in cui la divisione per zero si ottiene sostituendo il valore desiderato vengono convertite. Di seguito è riportato un esempio standard della divulgazione del limite mediante trasformazioni algebriche ordinarie:

Come si può vedere nell'esempio, una semplice riduzione della frazione si traduce nel suo valore in una risposta completamente razionale.

Quando si considerano i limiti delle funzioni trigonometriche, le loro espressioni tendono ad essere ridotte al primo limite notevole. Quando si considerano i limiti in cui il denominatore diventa 0 quando si imposta il limite, utilizzare il secondo limite notevole.

Metodo L'Hôpital

In alcuni casi, i limiti delle espressioni possono essere sostituiti dal limite dei loro derivati. Guillaume Lopital - Matematico francese, fondatore della scuola francese di analisi matematica. Ha dimostrato che i limiti delle espressioni sono uguali ai limiti delle derivate di queste espressioni. Nella scrittura matematica, la sua regola è la seguente.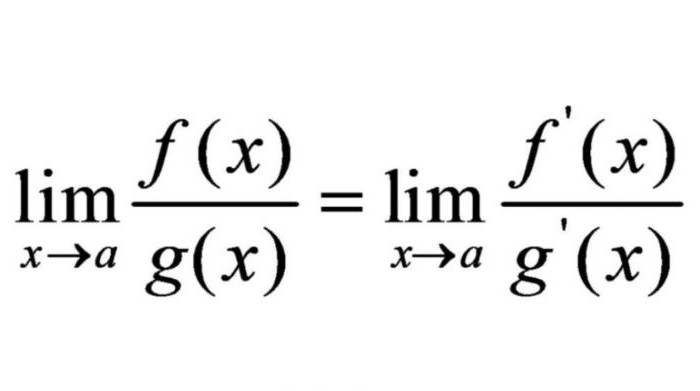

Attualmente, il metodo L'Hôpital viene utilizzato con successo per risolvere le incertezze del tipo 0: 0 o ∞: ∞.