Equazione di regressione Equazione di regressione multipla
Durante i loro studi, gli studenti incontrano spesso varie equazioni. Uno di questi, l'equazione di regressione, è considerato in questo articolo. Questo tipo di equazione viene utilizzato specificamente per descrivere le caratteristiche della relazione tra parametri matematici. Questo tipo di uguaglianza viene utilizzato in statistica ed econometria.
Definizione di regressione
In matematica, la regressione si riferisce a un certo valore che descrive la dipendenza del valore medio della totalità dei dati dai valori di un altro valore. L'equazione di regressione mostra il valore medio di un altro attributo in funzione di un determinato attributo. La funzione di regressione ha la forma di una semplice equazione y = x, in cui y è la variabile dipendente e x è indipendente (fattore-segno). In effetti, la regressione è espressa come y = f (x).
Ad
Quali sono i tipi di relazioni tra le variabili?
In generale, spiccano due tipi opposti di interconnessione: correlazione e regressione.
Il primo è caratterizzato dall'uguaglianza di variabili condizionali. In questo caso, non è noto attendibilmente quale variabile dipende da un'altra.
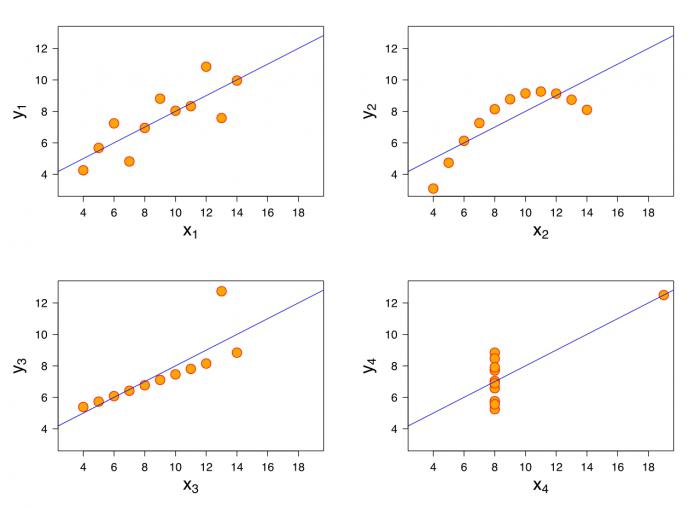
Se non c'è un'uguaglianza tra le variabili e nelle condizioni in cui viene detto quale variabile spiega e quale è dipendente, allora possiamo parlare della presenza di un secondo tipo di connessione. Per costruire un'equazione di regressione lineare, sarà necessario capire quale tipo di relazione viene osservata.
Tipi di regressioni
Ad oggi, ci sono 7 diversi tipi di regressione: iperbolica, lineare, multipla, non lineare, vapore, inversa, logaritmicamente lineare.
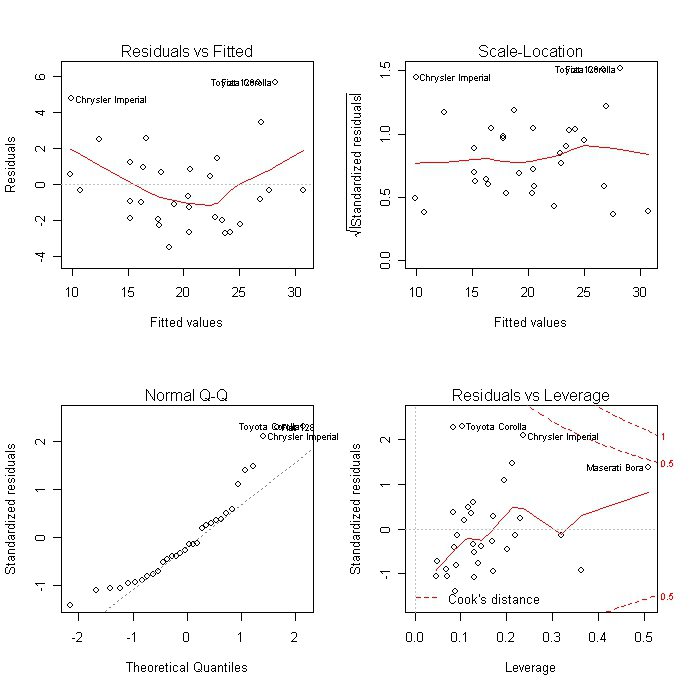
Iperbolico, lineare e logaritmico
Equazione lineare Le regressioni sono utilizzate nelle statistiche per spiegare chiaramente i parametri dell'equazione. Sembra y = c + t * x + e. L'equazione iperbolica ha la forma di un'iperbole regolare: y = c + t / x + E. Un'equazione logaritmicamente lineare esprime una relazione usando una funzione logaritmica: In y = In c + t * In x + In E.
Ad
Plurale e non lineare
Due tipi più complessi di regressione sono multipli e non lineari. L'equazione di regressione multipla è espressa dalla funzione y = f (x 1 , x 2 ... x c ) + E. In questa situazione, y è la variabile dipendente e x è la variabile esplicativa. La variabile E è stocastica, include l'influenza di altri fattori nell'equazione. L'equazione di regressione non lineare è un po 'contraddittoria. Da un lato, rispetto agli indicatori presi in considerazione, non è lineare, ma d'altro canto, nel ruolo di valutare gli indicatori, è lineare.
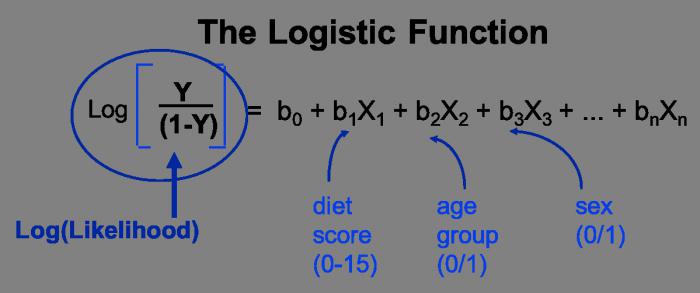
Tipi di regressioni inverse e accoppiate
L'inverso è un tipo di funzione che deve essere convertita in una forma lineare. Nei programmi applicativi più tradizionali, ha la forma di una funzione y = 1 / s + t * x + E. L'equazione di regressione a coppie dimostra la relazione tra i dati come una funzione di y = f (x) + E. Proprio come in altre equazioni, y dipende da x, ed E è un parametro stocastico.
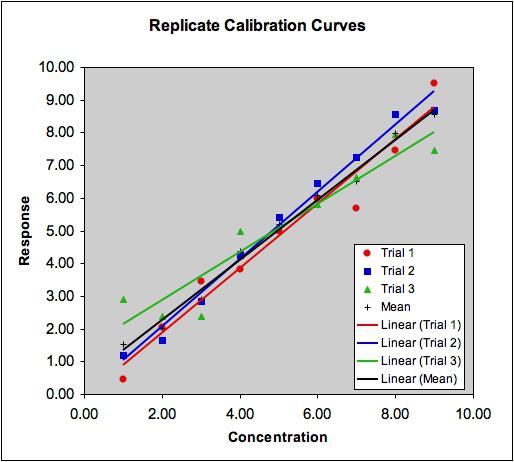
Il concetto di correlazione
Questo è un indicatore che dimostra l'esistenza di una relazione tra due fenomeni o processi. La forza della relazione è espressa come coefficiente di correlazione. Il suo valore oscilla all'interno dell'intervallo [-1; +1]. Un indicatore negativo indica la presenza di feedback, uno positivo indica uno diretto. Se il coefficiente assume il valore 0, non vi è alcuna relazione. Più il valore è vicino a 1, più forte è la connessione tra i parametri, più vicino a 0, più debole.
Ad
metodi
I metodi parametrici di correlazione possono valutare la vicinanza della relazione. Vengono utilizzati sulla base della stima della distribuzione per studiare i parametri che rispettano la legge della distribuzione normale.
I parametri dell'equazione di regressione lineare sono necessari per identificare il tipo di dipendenza, la funzione dell'equazione di regressione e la valutazione degli indicatori della formula di interrelazione scelta. Il campo di correlazione viene utilizzato come metodo di identificazione della comunicazione. Per fare ciò, tutti i dati esistenti devono essere visualizzati graficamente. In un sistema di coordinate bidimensionale rettangolare è necessario applicare tutti i dati noti. Questo forma un campo di correlazione. Il valore del fattore descrittivo è marcato lungo l'asse delle ascisse, mentre i valori del fattore dipendente sono marcati lungo l'asse delle ordinate. Se esiste una relazione funzionale tra i parametri, essi sono disposti sotto forma di una linea.
Se il coefficiente di correlazione di tali dati è inferiore al 30%, si può parlare della quasi completa assenza di comunicazione. Se è compreso tra il 30% e il 70%, questo indica la presenza di collegamenti di media tenuta. Indicatore 100% - evidenza di comunicazione funzionale.
L'equazione di regressione non lineare, così come quella lineare, deve essere integrata con un indice di correlazione (R).
Correlazione multipla della regressione
Il coefficiente di determinazione è un indicatore del quadrato di correlazione multipla. Parla della vicinanza della relazione dell'insieme di indicatori presentato con il tratto studiato. Può anche parlare della natura dell'influenza dei parametri sul risultato. L'equazione di regressione multipla è stimata usando questo indicatore.
Ad
Per calcolare l'indice di correlazione multipla, è necessario calcolare il suo indice.
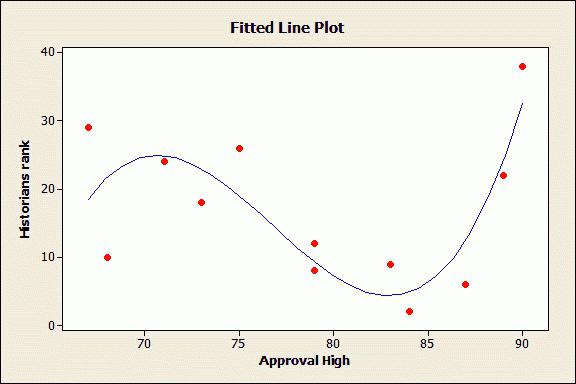
Metodo dei minimi quadrati
Questo metodo è un metodo per stimare i fattori di regressione. La sua essenza sta nel minimizzare la somma delle deviazioni nel quadrato, ottenuta a causa della dipendenza del fattore dalla funzione.
L'equazione di regressione lineare a coppie può essere stimata usando questo metodo. Questo tipo di equazioni viene utilizzato nel caso di rilevamento tra indicatori di una relazione lineare a coppie.
Parametri di equazioni
Ogni parametro della funzione di regressione lineare ha un significato specifico. L'equazione di regressione lineare accoppiata contiene due parametri: s e m. Il parametro t mostra la variazione media nell'indicatore finale della funzione y, soggetta a una diminuzione (aumento) della variabile x di un'unità convenzionale. Se la variabile x è zero, la funzione è uguale al parametro c. Se la variabile x non è zero, allora il fattore c non ha un senso economico. L'unica influenza sulla funzione ha un segno davanti al fattore c. Se c'è un segno negativo, allora possiamo dire del cambiamento lento nel risultato rispetto al fattore. Se c'è un vantaggio, allora questo indica un cambiamento accelerato nel risultato.
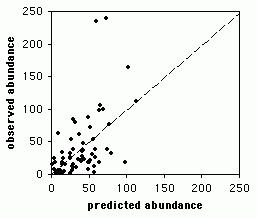
Ogni parametro che modifica il valore dell'equazione di regressione può essere espresso tramite l'equazione. Ad esempio, il fattore c ha la forma c = y - mx.
Dati raggruppati
Vi sono tali condizioni del problema in cui tutte le informazioni sono raggruppate sulla base di x, ma i corrispondenti valori medi dell'indicatore dipendente sono indicati per un particolare gruppo. In questo caso, i valori medi descrivono come l'indice, a seconda di x, cambia. Pertanto, le informazioni raggruppate aiutano a trovare un'equazione di regressione. È usato come analisi delle relazioni. Tuttavia, questo metodo ha i suoi svantaggi. Sfortunatamente, gli indicatori medi sono spesso soggetti a fluttuazioni esterne. Queste oscillazioni non riflettono il modello di relazione, ma mascherano solo il suo "rumore". Le medie mostrano che i modelli di relazione sono molto peggiori dell'equazione di regressione lineare. Tuttavia, possono essere usati come base per trovare l'equazione. Moltiplicando la forza di una singola popolazione per la media corrispondente, è possibile ottenere la quantità di y all'interno del gruppo. Successivamente, è necessario allineare tutti gli importi ricevuti e trovare l'indicatore finale di. Un po 'più difficile fare calcoli con la somma di xy. In tal caso, se gli intervalli sono piccoli, puoi condizionalmente assumere l'indicatore x per tutte le unità (all'interno del gruppo) allo stesso modo. È necessario moltiplicarlo con la somma y, per scoprire la somma dei prodotti x per y. Inoltre, tutte le quantità vengono sommate e viene ottenuta la quantità totale xy.
Ad
Equazione di regressione a coppie multiple: stimare l'importanza della comunicazione
Come precedentemente discusso, la regressione multipla ha una funzione della forma y = f (x 1 , x 2 , ..., x m ) + E. Molto spesso, tale equazione viene utilizzata per risolvere il problema della domanda e dell'offerta di un prodotto, degli interessi su azioni riacquistate, per studiare le cause e il tipo di funzione dei costi di produzione. È anche attivamente utilizzato in un'ampia varietà di studi e calcoli macroeconomici, ma a livello microeconomico, tale equazione è usata un po 'meno.
Il compito principale della regressione multipla è quello di costruire un modello di dati contenente un enorme quantità di informazioni al fine di determinare ulteriormente l'impatto di ciascuno dei fattori separatamente e nella loro totalità totale sull'indicatore da modellare e i suoi coefficienti. L'equazione di regressione può assumere un'ampia varietà di valori. Allo stesso tempo, vengono comunemente usati due tipi di funzioni per valutare l'interconnessione: lineare e non lineare.
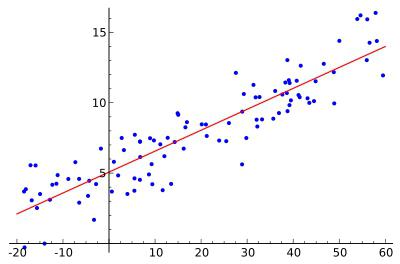
La funzione lineare è rappresentata nella forma della seguente relazione: y = a 0 + a 1 x 1 + a 2 x 2 , + ... + a m x m . Allo stesso tempo, a2, a m , sono considerati coefficienti di regressione "puri". Sono necessari per caratterizzare il cambiamento medio nel parametro y con una variazione (diminuzione o aumento) in ciascun parametro corrispondente x di una unità, con la condizione di un valore stabile di altri indicatori.
Le equazioni non lineari, ad esempio, hanno la forma di una funzione di potenza y = ax 1 b1 x 2 b2 ... x m bm . In questo caso, vengono chiamati gli indicatori b 1 , b 2 ..... b m coefficienti di elasticità essi dimostrano come il risultato cambia (di quanto%) con un aumento (diminuzione) nell'indicatore corrispondente x dell'1% e con un indicatore stabile dei fattori rimanenti.
Quali fattori devono essere considerati quando si costruisce la regressione multipla
Al fine di costruire correttamente regressione multipla, è necessario scoprire quali fattori dovrebbero essere prestati particolare attenzione.
È necessario avere una certa comprensione della natura della relazione tra fattori economici e modelli. I fattori che devono essere inclusi sono necessari per rispondere ai seguenti criteri:
- Dovrebbe essere soggetto a quantificazione. Per utilizzare un fattore che descrive la qualità dell'oggetto, in ogni caso, dovrebbe essere fornita una forma quantitativa.
- Non dovrebbero esserci intercorrelazioni di fattori o una relazione funzionale. Tali azioni portano spesso a conseguenze irreversibili - il sistema di equazioni ordinarie diventa incondizionato, e ciò comporta la sua inaffidabilità e la vaghezza delle stime.
- Nel caso dell'esistenza di un enorme indicatore di correlazione, non c'è modo di determinare l'influenza isolata dei fattori sul risultato finale dell'indicatore, pertanto i coefficienti diventano non interpretati.
Metodi di costruzione
Esistono moltissimi metodi e metodi che spiegano come scegliere i fattori per un'equazione. Tuttavia, tutti questi metodi si basano sulla selezione dei coefficienti utilizzando l'indice di correlazione. Tra questi ci sono:
- Il metodo di eliminazione.
- Metodo di inclusione
- Analisi di regressione passo dopo passo.
Il primo metodo comporta l'eliminazione di tutti i coefficienti dal set cumulativo. Il secondo metodo prevede l'introduzione di molti fattori aggiuntivi. E il terzo è l'eliminazione dei fattori precedentemente utilizzati per l'equazione. Ognuno di questi metodi ha il diritto di esistere. Hanno i loro pro e contro, ma possono risolvere il problema di eliminare gli indicatori non necessari a modo loro. Di regola, i risultati ottenuti da ogni singolo metodo sono piuttosto vicini.
Metodi per l'analisi multivariata
Tali metodi per determinare i fattori sono basati sulla considerazione delle singole combinazioni di caratteristiche correlate. Includono analisi discriminante, riconoscimento facciale, il modo in cui i componenti principali e l'analisi del cluster. Inoltre, c'è anche analisi fattoriale tuttavia, è apparso a causa dello sviluppo del metodo componente. Tutti sono utilizzati in determinate circostanze, in base a determinate condizioni e fattori.