Cos'è l'accelerazione? Tipi di accelerazione. Formula. Un esempio di risoluzione del problema
La sezione della fisica responsabile dello studio delle caratteristiche del movimento nello spazio dei corpi è chiamata cinematica. In questo articolo consideriamo le quantità fisiche della cinematica utilizzate per descrivere il movimento degli oggetti e riveliamo anche quale sia l'accelerazione.
Grandezze fisiche in cinematica
Quando un corpo si muove nello spazio, è importante per noi sapere quale distanza percorre in un determinato periodo di tempo e lungo quale traiettoria si muove.
Per descrivere le distanze percorse in fisica, viene utilizzato il concetto di percorso - L. Nel caso del movimento lungo un cerchio, invece di un percorso, viene utilizzato il concetto di un angolo di rotazione θ. Il valore di L in SI è misurato in metri (m), e il valore di θ è misurato in radianti (rad.).
Oltre al percorso, è importante conoscere anche la velocità di movimento dei corpi. Sotto capisce la velocità del passaggio delle distanze. L'espressione matematica per la velocità lineare assume la forma:
v¯ = d L / dt
Per descrivere il movimento in un cerchio, applica la velocità angolare ω, che viene calcolata come segue:
ω¯ = d θ / dt
La terza importante quantità di cinematica è l'accelerazione.
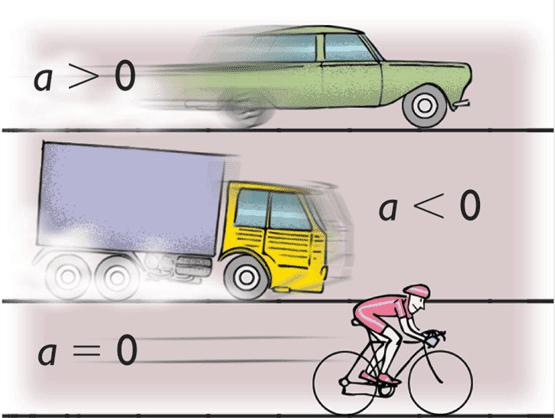
Cos'è l'accelerazione? Questa è una quantità in fisica, che mostra quanto rapidamente la velocità varia nel tempo. Matematicamente, questo può essere scritto come:
a¯ = d v¯ / dt
Se sostituiamo l'espressione per la velocità in questa formula di accelerazione, otteniamo:
a = d 2 L / dt 2
L'accelerazione è la prima derivata della velocità nel tempo o la seconda derivata nel tempo di viaggio.

Accelerazione tangenziale e normale
Sopra è stata data la definizione di accelerazione. Si chiama completo. Nel caso generale, la direzione della piena accelerazione non coincide con la direzione del vettore di velocità. Quest'ultimo è tangente alla traiettoria del movimento in nessuno dei suoi punti.
Poiché la velocità è una quantità vettoriale, cambiarla implica la possibilità di cambiare modulo e direzione. Nel primo caso, dicono che il corpo ha un'accelerazione tangenziale, nel secondo caso è normale.
Ad
La formula dell'accelerazione tangenziale a non differisce da quella per l'accelerazione completa a. La formula ha la forma:
a t = dv / dt
Cioè, tangenziale o tangenziale, come viene anche chiamato, l'accelerazione deriva dal modulo di velocità nel tempo. Il vettore a t ¯ coincide con il vettore v ¯ con movimento accelerato ed è opposto ad esso con movimento lento.
L'accelerazione normale è una quantità fisica che porta a una curvatura della traiettoria rettilinea dei corpi in movimento. È diretto lungo il raggio di curvatura della traiettoria, cioè normale rispetto ad essa. La formula per la sua definizione è:
a c = v 2 / r
L'accelerazione normale a c dipende dal modulo di velocità v e dal raggio di curvatura della traiettoria r. Ovviamente, nel caso del movimento lungo un raggio rettilineo, r può essere considerato uguale all'infinito. Quest'ultimo significa che l'accelerazione normale è zero per il movimento rettilineo.
Ad
Per il movimento circolare, il vettore a c è diretto al suo centro lungo il raggio. Per questo motivo, il valore di una c viene anche chiamato accelerazione centripeta.
Piena accelerazione
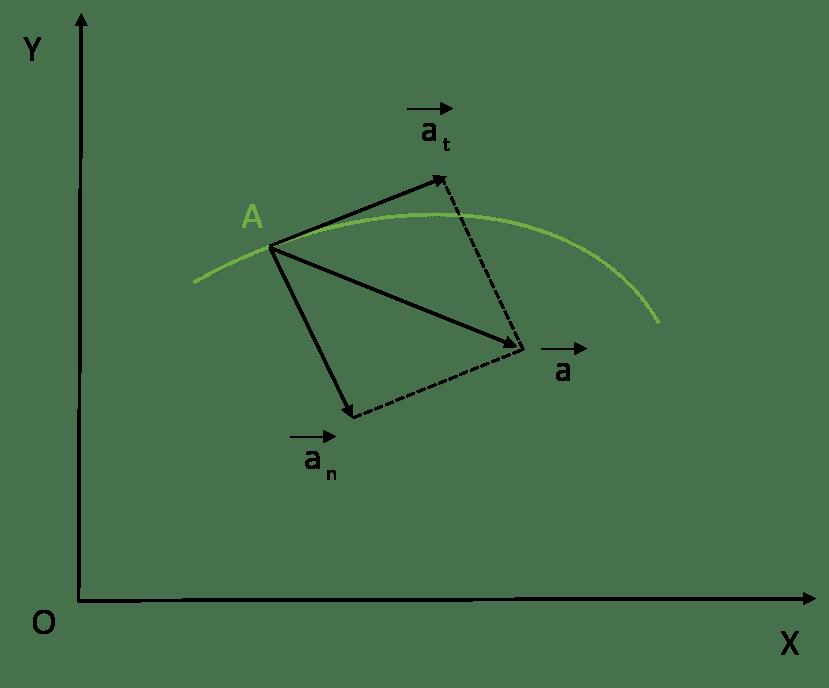
Il vettore di accelerazione totale è sempre la somma delle componenti tangenziali e normali. Poiché sono perpendicolari tra loro, il teorema di Pitagora può essere utilizzato per calcolare il modulo di accelerazione totale. La formula desiderata per l'accelerazione completa assume la forma:
a = √ (a t 2 + a c 2 )
Per determinare dove è diretto il vettore a ¯, è sufficiente calcolare l'angolo tra esso e qualsiasi componente. Ad esempio, l'angolo φ tra i vettori a e a t è uguale a:
φ = arctg (a c / a t )
Ricordiamo che l'accelerazione centripeta non è zero solo quando la curvatura della traiettoria del movimento è diversa dall'infinito. Nel caso del movimento rettilineo, l'accelerazione totale in magnitudine e direzione è uguale alla componente tangenziale.
Ad
Accelerazione angolare
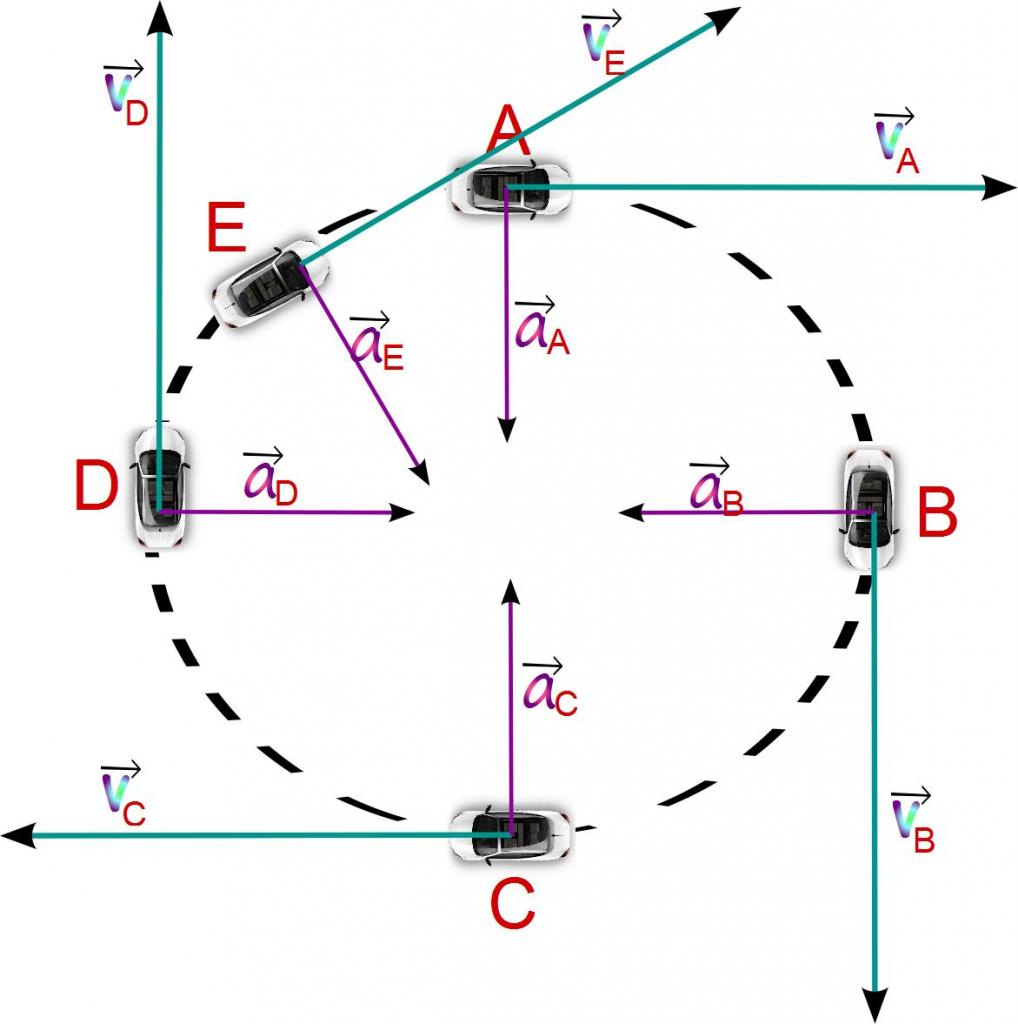
Considerando tale accelerazione, è necessario soffermarsi sulla corrispondente caratteristica angolare.
Sopra è stato introdotto il concetto di velocità angolare, che viene misurato in radianti al secondo (rad / s). Se troviamo la derivata di questa velocità rispetto al tempo, allora otteniamo la grandezza dell'accelerazione angolare:
α¯ = ω¯ / dt
È facile dimostrare che il valore angolare è correlato alla componente tangenziale dell'accelerazione completa dalla seguente relazione:
a t = α × r
Con l'accelerazione angolare costante, la componente tangente a t sarà maggiore per i punti più lontani dall'asse di rotazione.
L'accelerazione angolare non ha nulla a che fare con il componente normale.
Risolvere il problema di determinare l'accelerazione
Supponiamo che, muovendosi con costante di accelerazione lungo una linea retta, il corpo abbia percorso una distanza di 100 metri. È noto che la velocità iniziale del corpo era di 1 m / s. Il corpo ha percorso la distanza segnata in 5,5 secondi. Qual è l'accelerazione del movimento?
Ad
In base alla condizione del problema, stiamo parlando di moto uniformemente accelerato lungo una traiettoria diritta. Il percorso percorso in questo caso può essere calcolato con la formula:
L = v 0 × t + a × t 2/2
Esprimendo dall'uguaglianza il valore di a, abbiamo:
a = 2 × (L - v 0 × t) / t 2
Tutti i valori nella parte destra dell'uguaglianza sono noti dalla condizione. Sostituiscili e scrivi la risposta: a = 6,25 m / s 2 . Cioè, durante ciascuno di 5,5 secondi, la velocità del corpo aumenta di 6,25 m / s. Il valore trovato dell'accelerazione totale coincide con la componente tangenziale.