Qual è la costante gravitazionale?
Dopo aver studiato il corso di fisica nelle menti degli studenti ci sono tutti i tipi di permanenti e i loro valori. Il tema della gravità e della meccanica non fa eccezione. Molto spesso, non possono rispondere alla domanda su quanto sia importante la costante gravitazionale. Ma risponderanno sempre inequivocabilmente che è presente nella legge dell'ampiezza del mondo.
Dalla storia della costante gravitazionale
È interessante notare che nelle opere di Newton non esiste una tale grandezza. È apparsa in fisica molto più tardi. Più specificamente, fu solo all'inizio del XIX secolo. Ma questo non significa che non lo fosse. Gli scienziati semplicemente non l'hanno identificato e non ne hanno riconosciuto il significato esatto. A proposito di significato. gravità costante costantemente come è specificato decimale con un numero elevato di cifre dopo il punto decimale, davanti al quale è uno zero.
Ad
È proprio perché questa quantità assume un valore così piccolo che l'effetto delle forze di gravità è impercettibile sui piccoli corpi. Proprio a causa di questo moltiplicatore, la forza di attrazione risulta essere trascurabile.
Per la prima volta, stabilì sperimentalmente il valore assunto dalla costante gravitazionale, il fisico G. Cavendish. Ed è successo nel 1788.

Nei suoi esperimenti ha usato una verga sottile. Era sospeso su un filo di rame sottile e aveva una lunghezza di circa 2 metri. Alle estremità di questa asta sono state attaccate due sfere identiche di piombo con un diametro di 5 cm, accanto a cui sono state installate grandi sfere di piombo. Il loro diametro era già di 20 cm.
All'avvicinarsi di sfere grandi e piccole, è stata osservata una rotazione dell'asta. Ha parlato della loro attrazione. Dalle masse e dalla distanza conosciute, nonché dalla forza di torsione misurata, è stato possibile scoprire con precisione quale sia la costante gravitazionale uguale.
Ad
Tutto è iniziato con una caduta libera di corpi.
Se mettiamo i corpi di massa diversa nel vuoto, allora cadranno allo stesso tempo. A condizione che cadano dalla stessa altezza e inizino contemporaneamente. È stato possibile calcolare l'accelerazione con cui tutti i corpi cadono sulla Terra. Risultò approssimativamente pari a 9,8 m / s 2 .
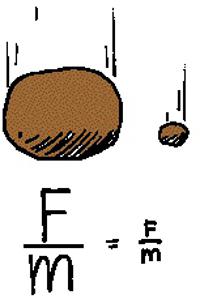
Gli scienziati hanno scoperto che la forza con cui tutto è attratto dalla Terra è sempre presente. E non dipende dall'altezza a cui si muove il corpo. Un metro, un chilometro o centinaia di chilometri. Non importa quanto lontano sia il corpo, sarà attratto dalla Terra. Un'altra domanda è come il suo valore dipenderà dalla distanza?
Fu a questa domanda che il fisico inglese I. Newton trovò la risposta.
Riducendo la forza di attrazione dei corpi con la loro distanza
Per cominciare, ha suggerito che la forza di gravità diminuisce. E il suo valore è inversamente proporzionale alla distanza al quadrato. Inoltre, questa distanza deve essere contata dal centro del pianeta. E ha fatto calcoli teorici.
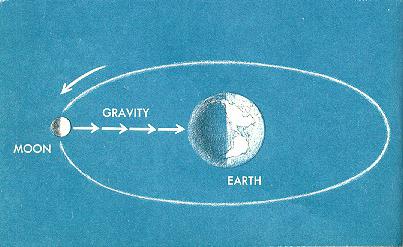
Quindi questo scienziato ha usato i dati degli astronomi sul movimento del satellite naturale della Terra: la Luna. Newton calcolò l'accelerazione con cui ruotava attorno al pianeta e ottenne gli stessi risultati. Ciò testimoniava la veridicità del suo ragionamento e permetteva di formulare la legge del mondo. La costante gravitazionale nella sua formula è stata finora assente. In questa fase era importante determinare la dipendenza. Cosa è stato fatto La gravità diminuisce inversamente alla distanza quadrata quadrata dal centro del pianeta.
Ad
Alla legge del mondo
Newton continuò a pensare. Poiché la Terra attrae la Luna, allora essa stessa dovrebbe essere attratta dal Sole. Inoltre, la forza di tale attrazione dovrebbe anche obbedire alla legge da lui descritta. E poi Newton lo ha diffuso a tutti i corpi dell'universo. Pertanto, il nome della legge include la parola "universale".
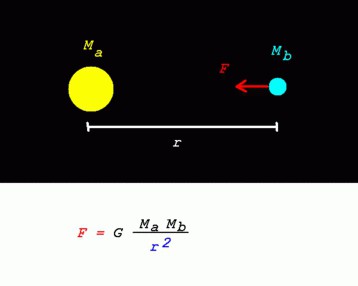
Le forze dei corpi di tutto il mondo sono definite come proporzionalmente dipendenti dal prodotto delle masse e inverse rispetto al quadrato della distanza. Successivamente, quando il coefficiente è stato determinato, la formula della legge ha acquisito la seguente forma:
- F t = G (m 1 * x m 2 ): r 2 .
Contiene la seguente notazione:
| forza di gravità | F t |
| Costante gravitazionale | sol |
| Massa corporea | m 1 , m 2 |
| Distanza tra i corpi | r |
La formula per la costante gravitazionale segue da questa legge:
- G = (F t X r 2 ): (m 1 x m 2 ).
Il valore della costante gravitazionale
Ora è arrivato il turno di numeri specifici. Poiché gli scienziati costantemente chiariscono questo valore, diversi numeri sono stati adottati ufficialmente in anni diversi. Ad esempio, secondo i dati per il 2008, la costante gravitazionale è 6,6742 x 10 -11 Nˑm 2 / kg 2 . Sono passati tre anni e la costante viene contata. Ora la costante gravitazionale è 6,6738 x 10 -11 Nˑm 2 / kg 2 . Ma per gli alunni nella risoluzione dei problemi è ammesso il suo arrotondamento a tale valore: 6,67 x 10 -11 Nm 2 / kg 2 .
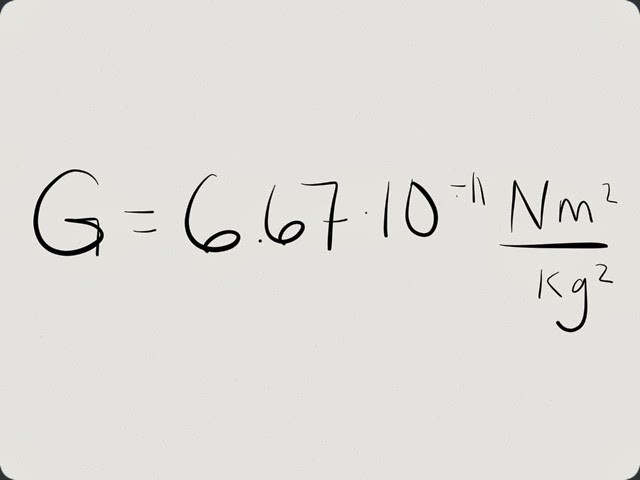
Qual è il significato fisico di questo numero?
Se nella formula, che è data per la legge del mondo, per sostituire numeri concreti, ottieni un risultato interessante. Nel caso particolare, quando le masse dei corpi sono pari a 1 chilogrammo e si trovano ad una distanza di 1 metro, la forza della forza è uguale al numero stesso, che è noto per la costante gravitazionale.
Ad
Cioè, il significato della costante gravitazionale è che mostra con quale forza tali corpi saranno attratti ad una distanza di un metro. Per numero puoi vedere quanto è piccola questa forza. Dopo tutto, sono dieci miliardi in meno di uno. È persino impossibile notare. Anche con un aumento del corpo un centinaio di volte il risultato non cambierà in modo significativo. Rimane ancora molto meno di uno. Pertanto, diventa chiaro perché la forza di attrazione è evidente solo in quelle situazioni se almeno un corpo ha una massa enorme. Ad esempio, un pianeta o una stella.
Come è la costante gravitazionale con accelerazione caduta libera?
Se confrontiamo due formule, una delle quali sarà per la gravità e l'altra per la legge della Terra, possiamo vedere un modello semplice. La costante gravitazionale, la massa della Terra e il quadrato della distanza dal centro del pianeta costituiscono un coefficiente che è uguale a accelerare la caduta libera. Se scrivi questa formula, ottieni quanto segue:
- g = (G x M): r 2 .
E usa la seguente notazione:
| Massa terrestre | M |
| Raggio di terra | r |
A proposito, la costante gravitazionale può essere trovata da questa formula:
- G = (g x r 2 ): M.
Se vuoi conoscere l'accelerazione della caduta libera ad una certa altezza sopra la superficie del pianeta, allora questa formula è utile:
- g = (G x M): (r + n) 2 , dove n è l'altezza sopra la superficie della terra.
Compiti che richiedono la conoscenza della costante gravitazionale
Primo compito
Condizioni. Qual è l'accelerazione della caduta libera su uno dei pianeti del sistema solare, ad esempio, su Marte? È noto che la sua massa è 6,23 · 10 23 kg, e il raggio del pianeta è 3,38 · 10 6 m.
La decisione Devi usare la formula che è stata scritta per la Terra. Solo per sostituire in esso i valori indicati nell'attività. Si scopre che l'accelerazione della caduta libera sarà uguale al prodotto di 6,67 x 10 -11 e 6,23 x 10 23 , che poi dovrà essere diviso in un quadrato di 3,38 · 10 6 . Nel numeratore, si ottiene un valore di 41,55 x 10 12 . E il denominatore sarà 11.42 x 10 12 . I gradi saranno ridotti, quindi per la risposta è sufficiente conoscere il quoziente di due numeri.
Risposta : 3,64 m / s 2 .
Compito due
Condizioni. Cosa bisogna fare con i corpi per ridurre la loro forza di gravità di 100 volte?
La decisione Poiché la massa dei corpi non può essere cambiata, la forza diminuirà a causa della loro rimozione l'una dall'altra. Un centinaio si ottiene dalla quadratura 10. Ciò significa che la distanza tra loro dovrebbe essere 10 volte maggiore.
Risposta : distanziali di 10 volte la distanza originale.