Valore vettoriale in fisica: definizione, designazione, esempi
In matematica, un vettore è un segmento diretto di una certa lunghezza. In fisica, una quantità vettoriale è intesa come la caratteristica completa di una certa quantità fisica che ha un modulo e una direzione di azione. Considerare le proprietà di base dei vettori, nonché esempi di quantità fisiche che sono vettoriali.
Scalari e vettori
Gli scalari in fisica sono parametri che possono essere misurati e rappresentati da un singolo numero. Ad esempio, la temperatura, la massa e il volume sono scalari, poiché sono misurati dal numero di gradi, chilogrammo e metri cubi, rispettivamente.
Nella maggior parte dei casi, risulta che il numero che definisce il valore scalare non porta informazioni esaustive. Ad esempio, considerando tale caratteristica fisica come l'accelerazione, non sarà sufficiente dire che è 5 m / s 2 , perché è necessario sapere dove è diretto, contro la velocità del corpo, con un certo angolo rispetto a questa velocità o altrimenti. Oltre all'accelerazione, la velocità è un esempio di una quantità vettoriale in fisica. Sono inclusi anche in questa categoria forza, forza del campo elettrico e molti altri.
Ad
Secondo la definizione di una quantità vettoriale come segmento diretto nello spazio, può essere rappresentato come un insieme di numeri (componenti di un vettore), se è visualizzato in un determinato sistema di coordinate. Molto spesso, in fisica e matematica, sorgono problemi che, per descrivere un vettore, richiedono la conoscenza dei suoi componenti (problemi su un piano) o tre (problemi nello spazio).
Definizione del vettore nello spazio n-dimensionale
Nello spazio n-dimensionale, dove n è un numero intero, il vettore sarà determinato in modo univoco se i suoi componenti n sono noti. Ogni componente rappresenta la coordinata della fine del vettore lungo l'asse corrispondente di coordinate, a condizione che l'inizio del vettore sia all'inizio del sistema di coordinate dello spazio n-dimensionale. Di conseguenza, il vettore può essere rappresentato come: v = {a 1 , a 2 , a 3 , ..., a n }, dove a 1 è il valore scalare del primo componente del vettore v. Di conseguenza, in uno spazio tridimensionale, il vettore sarà scritto come v = {a 1 , a 2 , a 3 }, e in uno spazio bidimensionale - v = {a 1 , a 2 }.
Ad
Come viene indicato il valore del vettore? Qualsiasi vettore in spazi monodimensionali, bidimensionali e tridimensionali può essere rappresentato come un segmento diretto che si trova tra i punti A e B. In questo caso è indicato come AB → , dove la freccia indica che questo è un valore vettoriale. La sequenza di lettere può essere specificata dall'inizio del vettore fino alla sua fine. Ciò significa che se le coordinate dei punti A e B, ad esempio, in uno spazio tridimensionale, sono {x 1 , y 1 , z 1 } e {x 2 , y 2 , z 2 }, rispettivamente, allora le componenti del vettore AB → saranno uguali {x 2 -x 1 , y 2 -y 1 , z 2 -z 1 }.
Rappresentazione grafica del vettore
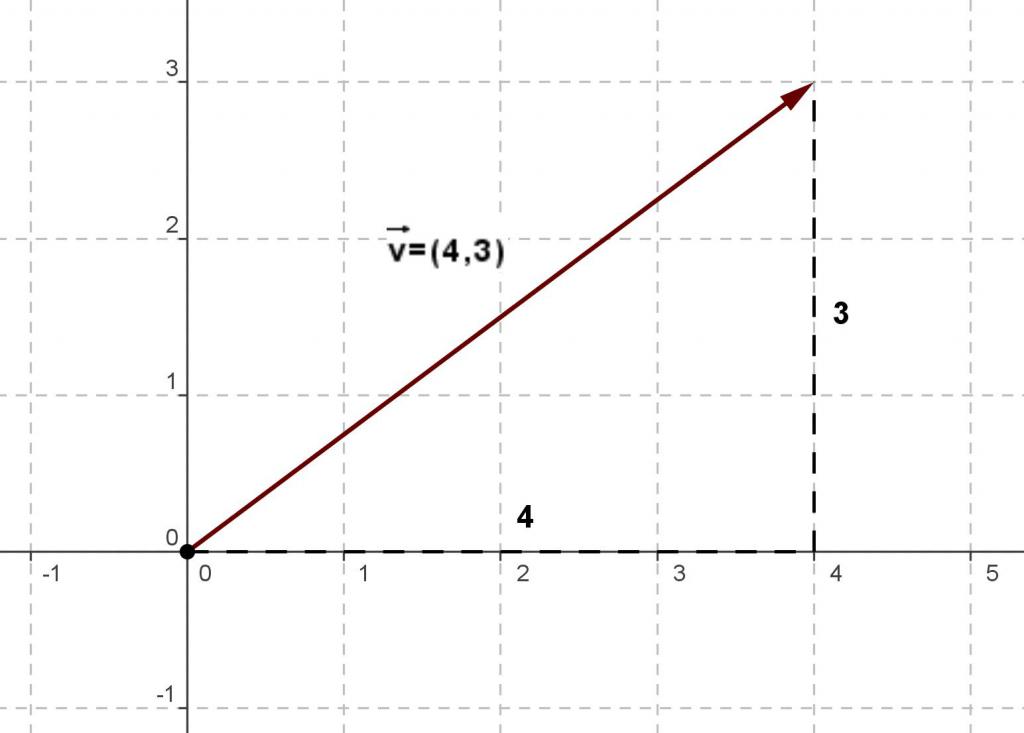
Nelle figure è consuetudine rappresentare una quantità vettoriale come un segmento, alla sua estremità c'è una freccia che indica la direzione della quantità fisica, la cui rappresentazione è. Questo segmento è solitamente firmato, ad esempio, v → o F → , in modo che sia chiaro quale caratteristica si intende.
Una rappresentazione grafica del vettore aiuta a capire dove viene applicata la quantità fisica e in quale direzione. Inoltre, è conveniente eseguire molte operazioni matematiche sui vettori usando le loro immagini.
Ad
Operazioni matematiche vettoriali
I valori vettoriali, così come i numeri ordinari, possono essere aggiunti, sottratti e moltiplicati sia tra loro che con altri numeri.
La somma di due vettori è il terzo vettore, che si ottiene se i parametri sommati sono posizionati in modo che la fine del primo coincida con l'inizio del secondo vettore e quindi connetta l'inizio del primo e la fine del secondo. Per eseguire questa azione matematica, sono stati sviluppati tre metodi principali:
- Il metodo del parallelogramma, che consiste nel costruire una figura geometrica su due vettori che provengono dallo stesso punto nello spazio. La diagonale di questo parallelogramma, che esce dal punto comune dell'inizio dei vettori, sarà la loro somma.
- Il metodo poligono, la cui essenza è che l'inizio di ogni vettore successivo dovrebbe essere posto alla fine del precedente, quindi il vettore totale collegherà l'inizio del primo e la fine dell'ultimo.
- Il metodo analitico, che consiste nell'addizione a coppie dei componenti corrispondenti dei vettori noti.
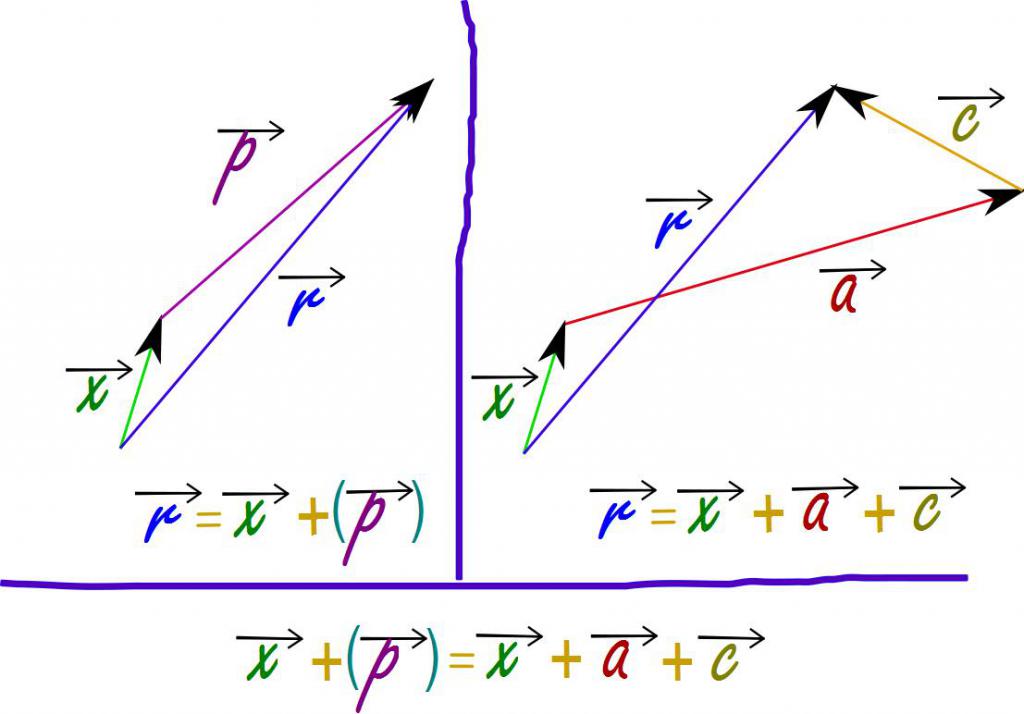
Per quanto riguarda la differenza delle grandezze vettoriali, può essere sostituita aggiungendo il primo parametro a quello opposto in direzione del secondo.
La moltiplicazione di un vettore di un certo numero A viene eseguita secondo una semplice regola: questo numero dovrebbe essere moltiplicato per ogni componente del vettore. Il risultato è anche un vettore il cui modulo è A volte quello originale, e la direzione è uguale o opposta a quella originale, tutto dipende dal segno del numero A.
Ad
È impossibile dividere un vettore o un numero in esso, ma la divisione di un vettore per il numero A è analoga alla moltiplicazione per il numero 1 / A.
Prodotto scalare e vettoriale
La moltiplicazione dei vettori può essere effettuata in due modi diversi: scalare e vettoriale.
Il prodotto scalare delle quantità vettoriali è chiamato un tale metodo di moltiplicazione, il cui risultato è un singolo numero, cioè uno scalare. Nella matrice, il prodotto scalare viene scritto come righe del componente del 1 ° vettore sulla colonna dei componenti del 2 °. Di conseguenza, nello spazio n-dimensionale otteniamo la formula: (A → * B → ) = a 1 * b 1 + a 2 * b 2 + ... + a n * b n .
In uno spazio tridimensionale, è possibile definire diversamente il prodotto scalare. Per fare ciò, moltiplica i moduli dei vettori corrispondenti per il coseno dell'angolo tra loro, cioè (A → * B → ) = | A → | * | B → | * cos (θ AB ). Da questa formula segue che se i vettori sono diretti in una direzione, allora il prodotto scalare è uguale alla moltiplicazione dei loro moduli, e se i vettori sono perpendicolari tra loro, allora risulta essere zero. Si noti che il modulo di un vettore in un sistema di coordinate rettangolari è definito come la radice quadrata della somma dei quadrati dei componenti di questo vettore.
Sotto il prodotto vettoriale capisci questa moltiplicazione di un vettore con un vettore, il cui risultato è anche un vettore. La sua direzione è perpendicolare a ciascuno dei parametri moltiplicati, e la lunghezza è uguale al prodotto dei moduli dei vettori e il seno dell'angolo tra loro, cioè A → x B → = | A → | * | B → | * sin (θ AB ), dove x è denota un prodotto vettoriale. Nella matrice, questo tipo di lavoro è rappresentato come un determinante le cui righe sono i vettori elementari di un dato sistema di coordinate e le componenti di ciascun vettore.
Ad
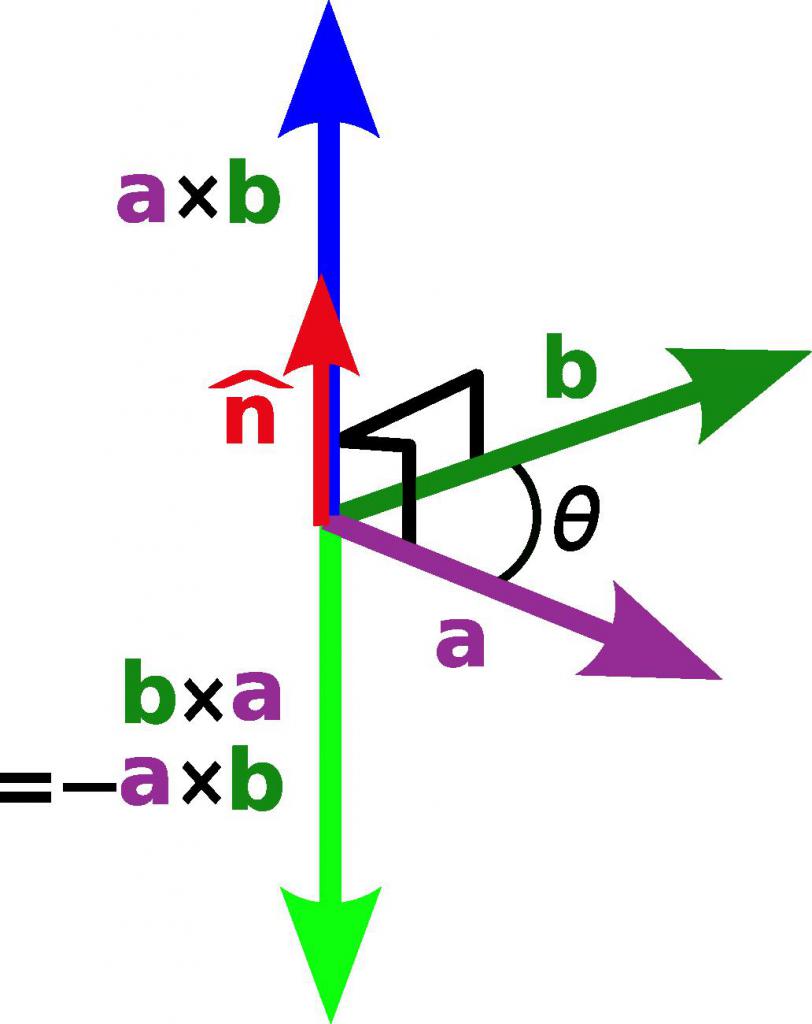
Entrambi i prodotti scalari e vettoriali sono utilizzati in matematica e fisica per determinare molte quantità, ad esempio l'area e il volume delle figure.
Il seguente articolo fornisce esempi di quantità vettoriali in fisica.
Velocità e accelerazione
La velocità in fisica è la velocità di cambiamento nella posizione di un dato punto materiale. La velocità nel sistema SI è misurata in metri al secondo (m / s) ed è indicata dal simbolo v → . Sotto l'accelerazione capisci la velocità del cambio di velocità. L'accelerazione è misurata in metri al secondo quadrato (m / s 2 ), ed è solitamente indicata dal simbolo a → . Il valore di 1 m / s 2 indica che per ogni secondo il corpo aumenta la sua velocità di 1 m / s.
La velocità e l'accelerazione sono quantità vettoriali che sono coinvolte nelle formule della seconda legge di Newton e nello spostamento del corpo come punto materiale. La velocità è sempre diretta lungo la direzione del movimento, mentre l'accelerazione può essere diretta arbitrariamente rispetto al corpo in movimento.
Forza fisica
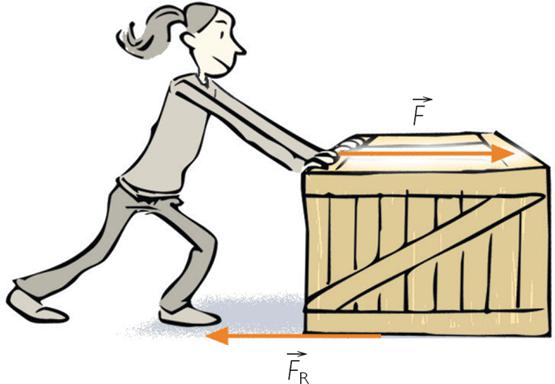
La forza è una quantità fisica vettoriale che riflette l'intensità dell'interazione tra i corpi. È indicato dal simbolo F → , misurato in newton (H). Per definizione, 1 N è una forza in grado di modificare la velocità di un corpo con una massa di 1 kg per 1 m / s per ogni secondo di tempo.
Questa quantità fisica è ampiamente usata in fisica, poiché è associata alle caratteristiche energetiche dei processi di interazione. La natura della forza può essere molto diversa, ad esempio, le forze gravitazionali dei pianeti, la forza che fa muovere l'auto, le forze elastiche dei mezzi solidi, le forze elettriche che descrivono il comportamento delle cariche elettriche, le forze magnetiche nucleari che determinano la stabilità dei nuclei atomici e così via.
Valore del vettore di pressione
Un altro valore è strettamente correlato al concetto di forza - pressione. In fisica, si intende la normale proiezione di forza sul sito su cui agisce. Poiché la forza è un vettore, quindi, secondo la regola di moltiplicare un numero per un vettore, la pressione sarà anche una quantità vettoriale: P → = F → / S, dove S è l'area. La pressione viene misurata in Pascal (Pa), 1 Pa è il parametro al quale la forza perpendicolare di 1 N agisce su una superficie di 1 m 2 . Sulla base della definizione, il vettore di pressione è diretto nella stessa direzione del vettore di forza.

In fisica, il concetto di pressione è spesso usato per studiare i fenomeni nei liquidi e nei gas (per esempio, la legge di Pascal o l'equazione di stato del gas ideale). La pressione è strettamente correlata alla temperatura corporea, poiché l'energia cinetica di atomi e molecole, la cui rappresentazione è la temperatura, spiega la natura dell'esistenza della pressione stessa.
Potenza del campo elettrico
C'è un campo elettrico attorno a qualsiasi corpo carico, la cui caratteristica di forza è la sua intensità. Questa intensità è definita come la forza che agisce in un dato punto del campo elettrico su una carica unitaria posta in questo punto. L'intensità del campo elettrico è indicata dalla lettera E → e viene misurata in newton per pendente (H / Cl). Il vettore di intensità è diretto lungo la linea del campo elettrico nella sua direzione, se la carica è positiva, e contro di essa, se la carica è negativa.
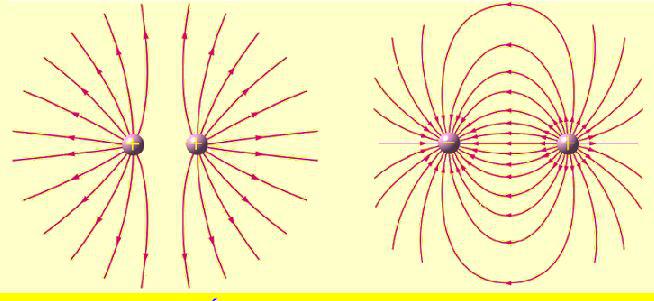
Il campo elettrico generato da una carica puntiforme può essere determinato in qualsiasi momento usando la legge di Coulomb.
Induzione magnetica
Il campo magnetico, come mostrato nel XIX secolo, gli scienziati Maxwell e Faraday, è strettamente connesso con il campo elettrico. Quindi, un campo elettrico mutevole genera un campo magnetico e viceversa. Pertanto, entrambi i tipi di campi sono descritti in termini di fenomeni fisici elettromagnetici.
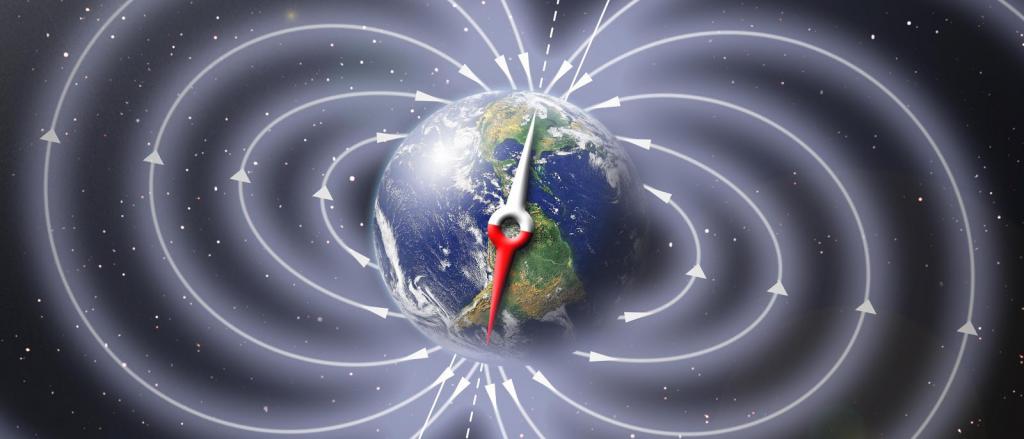
L'induzione magnetica descrive le proprietà di resistenza di un campo magnetico. L'induzione magnetica è un valore scalare o vettoriale? Puoi capire questo, sapendo che è definito attraverso la forza F → che agisce sulla carica q, che vola con la velocità v → in un campo magnetico, secondo la seguente formula: F → = q * | v → x B → |, dove B → - induzione magnetica. Quindi, rispondendo alla domanda se lo scalare o il vettore è l'induzione magnetica, si può dire che è un vettore che è diretto dal polo nord magnetico a quello sud. Misurato B → in tesla (T).
Candela fisica
Un altro esempio di una quantità vettoriale è la candela, che viene introdotta in fisica attraverso un flusso luminoso, misurato in lumen, passando attraverso una superficie delimitata da un angolo di 1 steradiante. Candela riflette la luminosità della luce, perché mostra la densità del flusso luminoso.