Trapezoidale rettangolare: tutte le formule e gli esempi di attività
I compiti con un trapezio non sembrano difficili in un numero di figure che sono state studiate in precedenza. Come caso speciale, viene considerato un trapezio rettangolare. E quando si cerca la sua area, a volte è più conveniente dividerlo in due già familiari: un rettangolo e un triangolo. Basta pensare un po 'e c'è una soluzione.
La definizione di un trapezio rettangolare e le sue proprietà
A un trapezio arbitrario, le basi sono parallele, e i lati possono avere un valore arbitrario degli angoli a loro. Se viene considerato un trapezio rettangolare, allora in esso uno dei lati è sempre perpendicolare alle basi. Cioè, i due angoli in esso saranno uguali a 90 gradi. Inoltre, appartengono sempre ai vertici adiacenti o, in altre parole, a un lato.
Ad
Altri angoli in un trapezio rettangolare sono sempre nitidi e ottusi. E la loro somma sarà sempre uguale a 180 gradi.
Ogni forma diagonale con il suo lato più piccolo triangolo rettangolo. E l'altezza, che è disegnata dall'alto con un angolo ottuso, divide la figura in due. Uno è un rettangolo e l'altro è un triangolo rettangolo. A proposito, questo lato è sempre uguale all'altezza del trapezio.
Quali designazioni sono accettate nelle formule presentate?
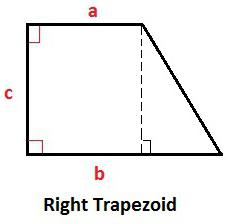
Tutti i valori utilizzati nelle diverse espressioni che descrivono un trapezio sono opportunamente specificati immediatamente e presentati nella tabella:
| valore | La sua designazione |
| un | base più grande |
| B | base più piccola di un trapezio rettangolare |
| c, h | perpendicolare al lato di base, altezza |
| d | lato inclinato |
| α | angolo acuto |
| β | angolo ottuso |
| m | linea centrale trapezio |
| d 1 | diagonale più piccola |
| d 2 | grande diagonale |
Formule che descrivono gli elementi di un trapezio rettangolare
Il più semplice di essi riguarda l'altezza e un lato più piccolo:
c = h.
Altre formule per questo lato di un trapezio rettangolare:
c = d * sinα;
c = (a - b) * tg α;
c = √ (d 2 - (a - b) 2 ).
Il primo segue da un triangolo rettangolo. E dice che la gamba dell'ipotenusa dà il seno dell'angolo opposto.
Nello stesso triangolo la seconda tappa è uguale alla differenza di due basi. Pertanto, un'affermazione che identifica la tangente di un angolo rispetto al rapporto delle gambe è vera.
Dallo stesso triangolo, si può ricavare una formula basata sulla conoscenza del teorema di Pitagora. Questa è la terza espressione registrata.
Le formule per l'altro lato possono essere scritte. Sono anche tre:
d = (a - b) / cosα;
d = c / sin α;
d = √ (c 2 + (a - b) 2 ).
I primi due vengono nuovamente ottenuti dalle proporzioni nello stesso triangolo rettangolo, e il secondo è derivato dal teorema di Pitagora.
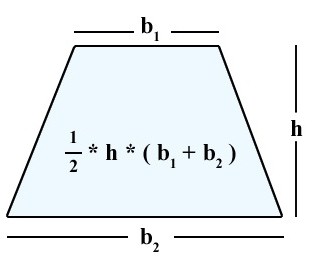
Quale formula può essere utilizzata per calcolare l'area?
Ciò che è dato per un trapezio arbitrario. Solo è necessario considerare che l'altezza è il lato perpendicolare alle basi.
S = (a + b) * h / 2.
Questi valori non sono sempre dati esplicitamente. Pertanto, per calcolare l'area di un trapezio rettangolare, è necessario eseguire alcuni calcoli matematici.
Cosa succede se hai bisogno di calcolare la diagonale?
In questo caso, è necessario vedere che formano due triangoli rettangoli. Quindi, puoi sempre usare il teorema di Pitagora. Quindi la prima diagonale sarà espressa come:
Ad
d1 = √ (c 2 + b 2 )
o in un altro modo, sostituendo "da" con "h":
d1 = √ (h 2 + b 2 ).
Allo stesso modo, si ottengono le formule per la seconda diagonale:
d2 = √ (c 2 + b 2 ) o d 2 = √ (h 2 + a 2 ).
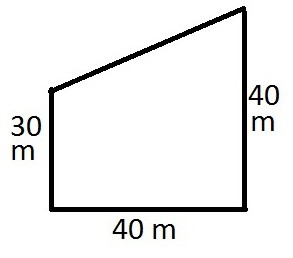
Problema numero 1
Condizioni. L'area di un trapezio rettangolare è nota ed è 120 dm 2 . La sua altezza è di 8 dm. È necessario calcolare tutti i lati del trapezio. Una condizione aggiuntiva è che una base è più piccola dell'altra di 6 dm.
La decisione Dato che viene dato un trapezio rettangolare, in cui è nota l'altezza, possiamo dire immediatamente che un lato è uguale a 8 dm, cioè il lato più piccolo.
Ora puoi contare l'altro: d = √ (con 2 + (a - b) 2 ). E qui vengono immediatamente indicati sia il lato con che la differenza delle basi. Quest'ultimo è 6 dm, questo è noto dalla condizione. Allora d sarà uguale radice quadrata da (64 + 36), cioè da 100. Quindi trovato un altro lato, pari a 10 dm.
Ad
La somma delle basi può essere trovata dalla formula per l'area. Sarà uguale al doppio del valore dell'area divisa per l'altezza. Se contate, risulta 240/8, quindi la somma delle basi è 30 dm. D'altra parte, la loro differenza è di 6 dm. Combinando queste equazioni, possiamo contare entrambe le basi:
a + b = 30 e a - b = 6.
Puoi esprimere un come (b + 6), sostituirlo nella prima uguaglianza. Quindi risulta che 2b sarà uguale a 24. Pertanto, solo b sarà 12 dm.
Quindi l'ultimo lato a è uguale a 18 dm.
La risposta è I lati di un trapezio rettangolare: a = 18 dm, b = 12 dm, c = 8 dm, d = 10 dm.
Problema numero 2
Condizioni. Dato un trapezio rettangolare. Il suo lato grande è uguale alla somma delle basi. La sua altezza è di 12 cm. Viene costruito un rettangolo, i cui lati sono uguali alla base del trapezio. È necessario calcolare l'area di questo rettangolo.
Ad
La decisione Devi iniziare con il desiderato. L'area richiesta è determinata come il prodotto di aeb. Entrambe queste quantità non sono note.
Sarà richiesto di utilizzare ulteriori uguaglianze. Uno di questi è basato sull'affermazione della condizione: d = a + b. È necessario usare la terza formula per questo lato, che è dato sopra. Risulta: d 2 = c 2 + (a - b) 2 o (a + b) 2 = c 2 + (a - b) 2 .
È necessario effettuare la trasformazione, sostituendo invece il suo valore dalla condizione - 12. Dopo aver aperto le parentesi e lanciato questi termini, risulta che 144 = 4 ab.
All'inizio della decisione, è stato detto che a * b fornisce l'area richiesta. Pertanto, nell'ultima espressione, è possibile sostituire questo prodotto con S. Un semplice calcolo fornirà il valore dell'area. S = 36 cm 2 .
La risposta è L'area richiesta è di 36 cm 2 .
Problema numero 3
Condizioni. L'area di un trapezio rettangolare di 150√3 cm². L'angolo acuto è di 60 gradi. L'angolo tra la base piccola e la diagonale più piccola ha lo stesso valore. È necessario calcolare la diagonale più piccola.
La decisione Dalla proprietà degli angoli trapezoidali, si scopre che il suo angolo ottuso è 120º. Quindi la diagonale la divide in uguale, perché una parte di esso è già di 60 gradi. Quindi l'angolo tra questa diagonale e la seconda base è anche di 60 gradi. Cioè, un triangolo formato da una grande base, un lato inclinato e una diagonale più piccola, è equilatero. Quindi, la diagonale desiderata sarà uguale a a, così come il lato d = a.
Ad
Ora dobbiamo considerare un triangolo rettangolo. In esso, il terzo angolo è di 30 gradi. Quindi la gamba che si trova contro di essa è uguale alla metà dell'ipotenusa. Cioè, la base più piccola del trapezio è uguale alla metà della diagonale desiderata: b = a / 2. Da esso è necessario trovare un'altezza uguale al lato, perpendicolare alle basi. Il lato con qui è una gamba. Dal teorema di Pitagora:
c = (a / 2) * √3.
Ora rimane solo per sostituire tutti i valori nella formula dell'area:
150√3 = (a + a / 2) * (a / 2 * √3) / 2.
Risolvendo questa equazione si ottiene una radice di 20
La risposta è La diagonale più piccola è lunga 20 cm.